Thinking With Mathematical Models Problem 2.4 Answers
The big news about chaos is supposed to be that the smallest of changes in a system can result in very large differences in that system's behavior. The so-called butterfly effect has become one of the most popular images of chaos. The idea is that the flapping of a butterfly's wings in Argentina could cause a tornado in Texas three weeks later. By contrast, in an identical copy of the world sans the Argentinian butterfly, no such storm would have arisen in Texas. The mathematical version of this property is known as sensitive dependence. However, it turns out that sensitive dependence is somewhat old news, so some of the implications flowing from it are perhaps not such "big news" after all. Still, chaos studies have highlighted these implications in fresh ways and led to thinking about other implications as well.
In addition to exhibiting sensitive dependence, chaotic systems possess two other properties: they are deterministic and nonlinear (Smith 2007). This entry discusses systems exhibiting these three properties and what their philosophical implications might be for theories and theoretical understanding, confirmation, explanation, realism, determinism, free will and consciousness, and human and divine action.
1. Defining Chaos: Determinism, Nonlinearity and Sensitive Dependence
The mathematical phenomenon of chaos is studied in sciences as diverse as astronomy, meteorology, population biology, economics and social psychology. While there are few (if any) causal mechanisms such diverse disciplines have in common, the phenomenological behavior of chaos—e.g., sensitivity to the tiniest changes in initial conditions or seemingly random and unpredictable behavior that nevertheless follows precise rules—appears in many of the models in these disciplines. Observing similar chaotic behavior in such diverse fields certainly presents a challenge to our understanding of chaos as a phenomenon.
1.1 A Brief History of Chaos
Arguably, one can say that Aristotle was already aware of something similar to what we now call sensitive dependence. Writing about methodology and epistemology, he observed that "the least initial deviation from the truth is multiplied later a thousandfold" (Aristotle OTH, 271b8). Nevertheless, thinking about how small disturbances might grow explosively to produce substantial effects on a physical system's behavior became a phenomenon of ever intensifying investigation beginning with a famous paper by Edward Lorenz (1963.) He noted that a particular meteorological model could exhibit exquisitely sensitive dependence on small changes in initial conditions. French mathematician Jacques Hadamard had already developed the framework for partial differential equations exhibiting both continuous and discontinuous dependence on initial conditions by 1922. Any equations exhibiting sensitive but continuous dependence are well-posed problems under his framework; however, he raised the possibility that any solution to equations for a physical system exhibiting such sensitive dependence could indicate that the target system obeyed no laws (Hadamard 1922, p. 38). Lorenz's pioneering work demonstrated that such sensitive dependence was not a matter of mathematical misdescription; rather, there was something interesting in the mathematical model exhibiting chaos. Moreover, Lorenz's and subsequent work indicated that there seemed to be no issue of the law-likeness of target systems whose models exhibited sensitive dependence.
Though some other scientists and mathematicians prior to Lorenz had examined such phenomena, these were basically isolated investigations never producing a recognizable, sustained field of inquiry as happened after the publication of Lorenz's seminal paper. Sensitive dependence on initial conditions (SDIC) for some systems had already been identified by James Clerk Maxwell (1876, p. 13). He described such phenomena as being cases where the "physical axiom" that from like antecedents flow like consequences is violated. Like others Maxwell recognized this kind of behavior could be found in systems with a sufficiently large number of variables (possessing a sufficient level of complexity in this numerical sense). But he also argued that such sensitive dependence could happen the case of two spheres colliding (1860). Henri Poincaré (1913), on the other hand, later recognized that this same kind of behavior could be realized in systems with a small number of variables (simple systems exhibiting very complicated behavior). Pierre Duhem, relying on work by Hadamard and Poincaré, further articulated the practical consequences of SDIC for the scientist interested in deducing mathematically precise consequences from mathematical models (1982, pp. 138–142).
Poincaré discussed examples that, in hindsight, we can view as raising doubts about taking explosive growth of small effects to be a sufficient condition for defining chaos. First, consider a perfectly symmetric cone precisely balanced on its tip with only the force of gravity acting on it. In the absence of any impressed forces, the cone would maintain this unstable equilibrium forever. It is unstable because the smallest nudge, from an air molecule, say, will cause the cone to tip over, but it could tip over in any direction due to the slight differences in various perturbations arising from suffering different collisions with different molecules. Here, variations in the slightest causes issue forth in dramatically different effects (a violation of Maxwell's physical axiom). If we were to plot the tipping over of the unstable cone, we would see that from a small ball of starting conditions, a number of different trajectories issuing forth from this ball would quickly diverge from each other.
The concept of nearby trajectories diverging or growing away from each other plays an important role in discussions of chaos. Three useful benchmarks for characterizing trajectory divergence are linear, exponential and geometric growth rates. Linear growth can be represented by the simple expression \(y = ax+b\), where \(a\) is an arbitrary positive constant and \(b\) is an arbitrary constant. A special case of linear growth is illustrated by stacking pennies on a checkerboard \((a = 1\), \(b = 0)\). If we use the rule of placing one penny on the first square, two pennies on the second square, three pennies on the third square, and so forth, we will end up with 64 pennies stacked on the last square. The total number of pennies on the checkerboard will be 2080. Exponential growth can be represented by the expression \(y = n_{0}e^{ax}\), where \(n_{0}\) is some initial quantity (say the initial number of pennies to be stacked) and \(a\) is an arbitrary positive constant. \((n_{0}\) is called 'initial' because when \(x = 0\) (the 'initial time'), we get \(y = n_{0}\).) Going back to our penny stacking analogy \((a = 1)\), we again start with placing 1 penny on the first square, but now about 2.7 pennies are stacked on the second square, about 7.4 pennies on the third square, and so forth, and we finally end up with about \(6.2 \times 10^{27}\) pennies staked on the last square! Clearly, exponential growth outpaces linear very rapidly. Finally, we have geometric growth, which can be represented by the expression \(y = a^{bx}\), where \(a\) and \(b\) are arbitrary positive constants. Note that in the case \(a = e\) and \(b = 1\), we recover the exponential case.[1]
Many authors consider an important mark of chaos to be trajectories issuing from nearby points diverging from one another exponentially quickly. However, it is also possible for trajectory divergence to be faster than exponential. Take Poincaré's example of a molecule in a gas of \(N\) molecules. If this molecule suffered the slightest of deviations from its initial starting point and you compared the molecule's trajectories from these two slightly different starting points, the resulting trajectories would diverge at a geometric rate, to the \(n\)th power, due to the \(n\) subsequent collisions, each being different than what it would have been had there been no slight change in the initial condition.
A third example discussed by Poincaré is of a man walking on a street on his way to his business. He starts out at a particular time. Meanwhile unknown to him, there is a tiler working on the roof of a building on the same street. The tiler accidentally drops a tile, killing the business man. Had the business man started out at a slightly earlier or later time, the outcome of his trajectory would have been vastly different!
1.2 Defining Chaos
Many intuitively think that the example of the business man is qualitatively different from Poincaré's other two examples and has nothing to do with chaos at all. However, the cone unstably balanced on its tip that begins to fall also is not a chaotic system as it has no other identifying features usually picked out as belonging to chaotic dynamics, such as nonlinear behavior (see below). Furthermore, it only has one unstable point—the tip—whereas chaos usually requires instability at nearly all points in a region (see below). To be able to identify systems as chaotic or not, we need a definition or a list of distinguishing characteristics. But coming up with a workable, broadly applicable definition of chaos has been problematic.
1.2.1 Dynamical Systems and Determinism
To begin, chaos is typically understood as a mathematical property of a dynamical system. A dynamical system is a deterministic mathematical model, where time can be either a continuous or a discrete variable. Such models may be studied as mathematical objects or may be used to describe a target system (some kind of physical, biological or economic system, say). I will return to the question of using mathematical models to represent actual-world systems throughout this article.
For our purposes, we will consider a mathematical model to be deterministic if it exhibits unique evolution:
(Unique Evolution)
A given state of a model is always followed by the same history of state transitions.
A simple example of a dynamical system would be the equations describing the motion of a pendulum. The equations of a dynamical system are often referred to as dynamical or evolution equations describing the change in time of variables taken to adequately describe the target system (e.g., the velocity as a function of time for a pendulum). A complete specification of the initial state of such equations is referred to as the initial conditions for the model, while a characterization of the boundaries for the model domain are known as the boundary conditions. An example of a dynamical system with a boundary condition would be the equation modeling the flight of a rubber ball fired at a wall by a small cannon. The boundary condition might be that the wall absorbs no kinetic energy (energy of motion) so that the ball is reflected off the wall with no loss of energy. The initial conditions would be the position and velocity of the ball as it left the mouth of the cannon. The dynamical system would then describe the flight of the ball to and from the wall.
Although some popularized discussions of chaos have claimed that it invalidates determinism, there is nothing inconsistent about systems having the property of unique evolution while exhibiting chaotic behavior (much of the confusion over determinism derives from equating determinism with predictability—see below). While it is true that apparent randomness can be generated if the state space (see below) one uses to analyze chaotic behavior is coarse-grained, this produces only an epistemic form of nondeterminism. The underlying equations are still fully deterministic. If there is a breakdown of determinism in chaotic systems, that can only occur if there is some kind of indeterminism introduced such that the property of unique evolution is rendered false (e.g., §4 below).
1.2.2 Nonlinear Dynamics
The dynamical systems of interest in chaos studies are nonlinear, such as the Lorenz model equations for convection in fluids:
\[\begin{align*} \frac{dx}{dt} &= -\sigma x + \sigma y; \\ \tag{Lorenz} \frac{dy}{dt} &= rx - y + xz ; \\ \frac{dz}{dt} &= xy - bz.\\ \end{align*}\]
A dynamical system is characterized as linear or nonlinear depending on the nature of the equations of motion describing the target system. Consider a differential equation system, such as \(d\bx/dt = \bF\bx\) for a set of variables \(\bx = x_1, x_2, \ldots, x_n\). These variables might represent positions, momenta, chemical concentration or other key features of the target system, and the system of equations tells us how these key variables change with time. Suppose that \(\bx_{1}(t)\) and \(\bx_{2}(t)\) are solutions of the equation system \(d\bx/dt = \bF\bx\). If the system of equations is linear, it can easily be shown that \(\bx_{3}(t) = a\bx_{1}(t)+ b\bx_{2}(t)\) is also a solution, where \(a\) and \(b\) are constants. This is known as the principle of linear superposition. So if the matrix of coefficients \(\bF\) does not contain any of the variables \(\bx\) or functions of them, then the principle of linear superposition holds. If the principle of linear superposition holds, then, roughly, a system behaves linearly: Any multiplicative change in a variable, by a factor \(\alpha\) say, implies a multiplicative or proportional change of its output by \(\alpha\). For example, if you start with your stereo at low volume and turn the volume control one unit, the volume increases by one unit. If you now turn the control two units, the volume increases two units. This is an example of a linear response. In a nonlinear system, such as (Lorenz), linear superposition fails and a system need not change proportionally to the change in a variable. If you turn your volume control too far, the volume may not only increase more than the number of units of the turn, but whistles and various other distortions occur in the sound. These are examples of a nonlinear response.
1.2.3 State Space and the Faithful Model Assumption
Much of the modeling of physical systems takes place in what is called state space, an abstract mathematical space of points where each point represents a possible state of the system. An instantaneous state is taken to be characterized by the instantaneous values of the variables considered crucial for a complete description of the state. One advantage of working in state space is that it often allows us to study useful geometric properties of the trajectories of the target system without knowing the exact solutions to the dynamical equations. When the state of the system is fully characterized by position and momentum variables, the resulting space is often called phase space. A model can be studied in state space by following its trajectory from the initial state to some chosen final state. The evolution equations govern the path—the history of state transitions—of the system in state space.
However, note that some crucial assumptions are being made here. We are assuming, for instance, that a state of a system is characterized by the values of the crucial variables and that a physical state corresponds via these values to a point in state space. These assumptions allow us to develop mathematical models for the evolution of these points in state space and such models are taken to represent (perhaps through an isomorphism or some more complicated relation) the physical systems of interest. In other words, we assume that our mathematical models are faithful representations of physical systems and that the state spaces employed faithfully represent the space of actual possibilities of target systems. This package of assumptions is known as the faithful model assumption (e.g., Bishop 2005), and, in its idealized limit—the perfect model scenario—it can license the (perhaps sloppy) slide between model talk and system talk (i.e., whatever is true of the model is also true of the target system and vice versa). In the context of nonlinear models, faithfulness appears to be inadequate (§3).
1.2.4 Qualitative Definitions of Chaos
The question of defining chaos is basically the question what makes a dynamical system such as (1) chaotic rather than nonchaotic. But this turns out to be a hard question to answer! Stephen Kellert defines chaos theory as "the qualitative study of unstable aperiodic behavior in deterministic nonlinear dynamical systems" (1993, p. 2). This definition restricts chaos to being a property of nonlinear dynamical systems (although in his (1993), Kellert is sometimes ambiguous as to whether chaos is only a behavior of mathematical models or of actual-world systems). That is, chaos is chiefly a property of particular types of mathematical models. Furthermore, Kellert's definition picks out two key features that are simultaneously present: instability and aperiodicity. Unstable systems are those exhibiting SDIC. Aperiodic behavior means that the system variables never repeat any values in any regular fashion. I take it that the "theory" part of his definition has much to do with the "qualitative study" of such systems, so let's leave that part for §2. Chaos, then, appears to be unstable aperiodic behavior in nonlinear dynamical systems.
This definition is both qualitative and restrictive. It is qualitative in that there are no mathematically precise criteria given for the unstable and aperiodic nature of the behavior in question, although there are some ways of characterizing these aspects (the notions of dynamical system and nonlinearity have precise mathematical meanings). Of course can one add mathematically precise definitions of instability and aperiodicity, but this precision may not actually lead to useful improvements in the definition (see below).
The definition is restrictive in that it limits chaos to be a property of mathematical models, so the import for actual physical systems becomes tenuous. At this point we must invoke the faithful model assumption—namely, that our mathematical models and their state spaces have a close correspondence to target systems and their possible behaviors—to forge a link between this definition and chaos in actual systems. Immediately we face two related questions here:
- How faithful are our models? How strong is the correspondence with target systems? This relates to issues in realism and explanation (§5) as well as confirmation (§3).
- Do features of our mathematical analyses, e.g., characterizations of instability, turn out to be oversimplified or problematic, such that their application to physical systems may not be useful?
Furthermore, Kellert's definition may also be too broad to pick out only chaotic behaviors. For instance, take the iterative map \(x_{n + 1} = cx_{n}\). This map obviously exhibits only orbits that are unstable and aperiodic. For instance, choosing the values \(c = 1.1\) and \(x_{0} = .5\), successive iterations will continue to increase and never return near the original value of \(x_{0}\). So Kellert's definition would classify this map as chaotic, but the map does not have any other properties qualifying it as chaotic. This suggests Kellert's definition of chaos would pick out a much broader set of behaviors than what is normally accepted as chaotic.
Part of Robert Batterman's (1993) discusses problematic definitions of chaos, namely, those that focus on notions of unpredictability. This certainly is neither necessary nor sufficient to distinguish chaos from sheer random behavior. Batterman does not actually specify an alternative definition of chaos. He suggests that exponential instability—the exponential divergence of two trajectories issuing forth from neighboring initial conditions (taken by many as the defining feature of SDIC)—is a necessary condition, but leaves it open as to whether it is sufficient.

Figure 1: The Lorenz Attractor
However, what does appear to pass as a crucial feature of chaos for Batterman—a definition if you will—is the presence of a kind of "stretching and folding" mechanism in the dynamics (see the discussion on p. 49 and figure 5 of his essay). Basically such a mechanism will cause some trajectories to converge rapidly while causing other trajectories to diverge rapidly. Such a mechanism would tend to cause trajectories issuing from various points in some small neighborhood of state space to mix and separate in rather dramatic ways. For instance, some initially neighboring trajectories on the Lorenz attractor (Figure 1) become separated, where some end up on one wing while others end up on the other wing rather rapidly. This stretching and folding is part of what leads to definitions of the distance between trajectories in state space as increasing (diverging) on average.
The presence of such a mechanism in the dynamics, Batterman believes, is a necessary condition for chaos. As such, this defining characteristic could be applied to both mathematical models and actual-world systems, though the identification of such mechanisms in target systems may be rather tricky.
1.2.5 Quantitative Definitions of Chaos
Let us start with the property of SDIC and distinguish weak and strong forms of sensitive dependence (somewhat following Smith 1998). Weak sensitive dependence can be characterized as follows. Consider the propagator, \(\bJ(\bx(t))\), a function that evolves trajectories \(\bx(t)\) in time (an example of a propagator is given in the Appendix). Let \(\bx(0)\) and \(\by(0)\) be initial conditions for two different trajectories. Then, weak sensitive dependence can be defined as
(WSD)
A system characterized by \(\bJ(\bx(t))\) has the property of weak sensitive dependence on its initial conditions if and only if \(\exists \varepsilon \gt 0\) \(\forall \bx(0)\) \(\forall \delta \gt 0\) \(\exists t\gt 0\) \(\exists \by(0)\), \(\abs{\bx(0) - \by(0)} \lt \delta\) and \(\abs{\bJ(\bx(t)) - \bJ(\by(t))} \gt \varepsilon.\)
The essential idea is that the propagator acts so that no matter how close together \(\bx(0)\) and \(\by(0)\) are the trajectory initiating from \(\by(0)\) will eventually diverge by \(\varepsilon\) from the trajectory initiating from \(\bx(0)\). However, WSD does not specify the rate of divergence (it is compatible with linear rates of divergence) nor does it specify how many points surrounding \(\bx(0)\) will give rise to diverging trajectories (it could be a set of any measure, e.g., zero).
On the other hand, chaos is usually characterized by a strong form of sensitive dependence:
(SD)
\(\exists \lambda\) such that for almost all points \(\bx(0)\), \(\forall \delta \gt 0\) \(\exists t\gt 0\) such that for almost all points \(\by(0)\) in a small neighborhood \((\delta)\) around \(\bx(0)\), \(\abs{\bx(0) - \by(0)}\lt \delta\) and \(\abs{\bJ(\bx(t)) - \bJ(\by(t))} \approx \abs{\bJ(\bx(0)) - \bJ(\by(0))}e^{\lambda t}\),
where the "almost all" caveat is understood as applying for all points in state space except a set of measure zero. Here, \(\lambda\) is interpreted as the largest global Lyapunov exponent (see the Appendix) and is taken to represent the average rate of divergence of neighboring trajectories issuing forth from some small neighborhood centered around \(\bx(0)\). Exponential growth is implied if \(\lambda \gt 0\) (convergence if \(\lambda \lt 0)\). In general, such growth cannot go on forever. If the system is bounded in space and in momentum, there will be limits as to how far nearby trajectories can diverge from one another.
Note that according to SD, Poincaré's first two examples would fail to qualify as characterizing a chaotic system (the first one exhibits an entire range of growth rates from zero to larger than exponential, while the second one exhibits growth larger than exponential). On the other hand, these examples do satisfy WSD.
One strategy for devising a definition for chaos is to begin with discrete maps and then generalize to the continuous case. For example, if one begins with a continuous system, by using a Poincaré surface of section—roughly, a two-dimensional plane is defined and one plots the intersections of trajectories with this plane—a discrete map can be generated. If the original continuous system exhibits chaotic behavior, then the discrete map generated by the surface of section will also be chaotic because the surface of section will have the same topological properties as the continuous system. Robert Devaney's influential definition of chaos (1989) was proposed in this fashion.
Let \(f\) be a function defined on some state space \(S\). In the continuous case, \(f\) would vary continuously on \(S\) and we might have a differential equation specifying how \(f\) varies. In the discrete case, \(f\) can be thought of as a mapping that can be iterated or reapplied a number of times. To indicate this, we can write \(f^{n}(x)\), meaning \(f\) is applied iteratively \(n\) times. For instance, \(f^{3}(x)\) would indicate \(f\) has been applied three times, thus \(f^{3}(x) = f(f(f(x)))\) (Robert May's classic 1976 review article has a nice discussion of this for the logistic map, \(x_{n + 1} = rx_{n}(1 - x_{n})\), which arises in modeling the dynamics of predator-prey relations, for instance.). Furthermore, let \(K\) be a subset of \(S\). Then \(f(K)\) represents \(f\) applied to the set of points \(K\), that is, \(f\) maps the set \(K\) into \(f(K)\). If \(f(K) = K\), then \(K\) is an invariant set under \(f\).
Now Devaney's definition of chaos can be stated as follows:
(Chaos\(_{d})\)
A continuous map \(f\) is chaotic if \(f\) has an invariant set \(K\subseteq S\) such that
- \(f\) satisfies WSD on \(K\),
- The set of points initiating periodic orbits are dense in \(K\), and
- \(f\) is topologically transitive on \(K\).
Topological transitivity is the following notion: consider open sets \(U\) and \(V\) around the points \(u\) and \(v\) respectively. Regardless how small \(U\) and \(V\) are, some trajectory initiating from \(U\) eventually visits \(V\). This condition roughly guarantees that trajectories starting from points in \(U\) will eventually fill \(S\) densely. Taken together, these three conditions represent an attempt to precisely characterize the kind of irregular, aperiodic behavior we expect chaotic systems to exhibit.
Devaney's definition has the virtues of being precise and compact. However, objections have been raised against it. Since the time he proposed his definition, it has been shown that (2) and (3) imply (1) if the set \(K\) has an infinite number of elements (see Banks et al. 1992), although this result does not hold for sets with finite elements. More to the point, the definition seems counterintuitive in that it emphasizes periodic orbits rather than aperiodicity, but the latter seems a much better characterization of chaos. After all, it is precisely the lack of periodicity that is characteristic of chaos. To be fair to Devany, however, he casts his definition in terms of unstable periodic points, the kind of points where trajectories issuing forth from neighboring points would exhibit WSD. If the set of unstable periodic points is dense in \(K\), then we have a guarantee that the kinds of aperiodic orbits characteristic of chaos will be abundant. Some have argued that (2) is not even necessary for characterizing chaos (e.g., Robinson 1995, pp. 83–4). Furthermore, nothing in Devaney's definition hints at the stretching and folding of trajectories, which appears to be a necessary condition for chaos from a qualitative perspective. Peter Smith (1998, pp. 176–7) suggests that Chaos\(_{d}\) is, perhaps, a consequence rather than a mark of chaos.
Another possibility for capturing the concept of the folding and stretching of trajectories so characteristic of chaotic dynamics is the following:
(Chaos\(_{h})\)
A discrete map \(f\) is chaotic if, for some iteration \(n \ge 1\), it maps the unit interval \(I\) into a horseshoe (see Figure 2).
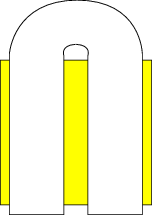
Figure 2: The Smale Horseshoe
To construct the Smale horseshoe map (Figure 2), start with the unit square (indicated in yellow). First, stretch it in the \(y\) direction by more than a factor of two. Then compress it in the \(x\) direction by more than a factor of two. Now, fold the resulting rectangle and lay it back onto the square so that the construction overlaps and leaves the middle and vertical edges of the initial unit square uncovered. Repeating these stretching and folding operations leads to the Samale attractor.
This definition has at least two virtues. First, it can be proven that Chaos\(_{h}\) implies Chaos\(_{d}\). Second, it yields exponential divergence, so we get SD, which is what many people expect for chaotic systems. However, it has a significant disadvantage in that it cannot be applied to invertible maps, the kinds of maps characteristic of many systems exhibiting Hamiltonian chaos. A Hamiltonian system is one where the total kinetic energy plus potential energy is conserved; in contrast, dissipative systems lose energy through some dissipative mechanism such as friction or viscosity. Hamiltonian chaos, then, is chaotic behavior in a Hamiltonian system.
Other possible definitions have been suggested in the literature. For instance (Smith 1998, pp. 181–2),
(Chaos\(_{te})\)
A discrete map is chaotic just in case it exhibits topological entropy: Let \(f\) be a discrete map and \(\{W_{i}\}\) be a partition of a bounded region \(W\) containing a probability measure which is invariant under \(f\). Then the topological entropy of \(f\) is defined as \(h_{T}(f) = \sup_{\{W_i\}h(f,\{W_i\})}\), where sup is the supremum of the set \(\{W_{i}\}\).
Roughly, given the points in a neighborhood \(N\) around \(\bx(0)\) less than \(\varepsilon\) away from each other, after \(n\) iterates of \(f\) the trajectories initiating from the points in \(N\) will differ by \(\varepsilon\) or greater, where more and more trajectories will differ by at least \(\varepsilon\) as \(n\) increases. In the case of one-dimensional maps, however, it can be shown that Chaos\(_{h}\) implies Chaos\(_{te}\). So this does not look to be a basic definition, though it is often more useful for proving theorems relative to the other definitions.
Another candidate, often found in the physics literature, is
(Chaos\(_{\lambda})\)
A discrete map is chaotic if it has a positive global Lyapunov exponent.
The meaning of positivity here is that a global Lyapunov exponent is positive for almost all points in the specified set \(S\). This definition certainly is directly connected to SD and is one physicists often use to characterize systems as chaotic. Furthermore, it offers practical advantages when it comes to calculations and can often be "straightforwardly" related to experimental data in the sense of examining data sets generated from physical systems for global Lyapunov exponents.[2]
1.2.6 Trouble with Lyapunov Exponents and Sensitive Dependence
One might think that SD, Chaos\(_{te}\) or Chaos\(_{\lambda}\) could be sufficient for defining chaos, but these characterizations run into problems from simple counterexamples. For instance, consider a discrete dynamical system with \(S = [0, \infty)\), the absolute value as a metric (i.e., as the function that defines the distance between two points) on \(\mathbf{R}\), and a mapping \(f: [(0, \infty) \rightarrow [0,\infty)\), \(f(x) = cx\), where \(c \gt 1\). In this dynamical system, all neighboring trajectories diverge exponentially fast, but all accelerate off to infinity. However, chaotic dynamics is usually characterized as being confined to some attractor—a strange attractor (see sec. 5.1 below) in the case of dissipative systems, the energy surface in the case of Hamiltonian systems. This confinement need not be due to physical walls of some container. If, in the case of Hamiltonian chaos, the dynamics is confined to an energy surface (by the action of a force like gravity), this surface could be spatially unbounded. So at the very least some additional conditions are needed (e.g., that guarantee trajectories in state space are dense).
In much physics and philosophy literature, something like the following set of conditions seems to be assumed as adequately defining chaos:
- Trajectories are confined due to some kind of stretching and folding mechanism.
- Some trajectory orbits are aperiodic, meaning that they do not repeat themselves on any time scales.
- Trajectories exhibit SD or Chaos\(_{\lambda}\).
Of these three features, (c) is often taken to be crucial to defining SDIC and is often suspected as being related to the other two. That is to say, exponential growth in the separation of neighboring trajectories characterized by \(\lambda\) is taken to be a property of a particular kind of dynamics that can only exist in nonlinear systems and models.
Though the favored approaches to defining chaos involve global Lyapunov exponents, there are problems with this way of defining SDIC (and, hence, characterizing chaos). First, the definition of global Lyapunov exponents involves the infinite time limit (see the Appendix), so, strictly speaking, \(\lambda\) only characterizes growth in uncertainties as \(t\) increases without bounds, not for any finite \(t\). So the combination \(\exists \lambda\) and \(\exists t\gt 0\) in SD is inconsistent. At best, SD can only hold for the large time limit and this implies that chaos as a phenomenon can only arise in this limit, contrary to what we take to be our best evidence. Furthermore, neither our models nor physical systems run for infinite time, but an infinitely long time is required to verify the presumed exponential divergence of trajectories issuing from infinitesimally close points in state space.
On might try to get around these problems by invoking the standard physicist's assumption that an infinite-time limit can be used to effectively represent some large but finite elapsed time. However, one reason to doubt this assumption in the context of chaos is that the calculation of finite-time Lyapunov exponents do not usually lead to on-average exponential growth as characterized by global Lyapunov exponents (e.g., Smith, Ziehmann and Fraedrich 1999). In general, for finite times the propagator varies from point to point in state space (i.e., it is a function of the position \(\bx(t)\) in state space and only approaches a constant in the infinite time limit), implying that the local finite-time Lyapunov exponents vary from point to point. Therefore, trajectories diverge and converge from each other at various rates as they evolve in time—the uncertainty does not vary uniformly in the chaotic region of state space (Smith, Ziehmann and Fraedrich 1999; Smith 2000). This is in contrast to global Lyapunov exponents which are on-average global measures of trajectory divergence and which imply that uncertainty grows uniformly (for \(\lambda \gt 0)\), but such uniform growth rarely occurs outside a few simple mathematical models. For instance, the Lorenz, Moore-Spiegel, Rössler, Henon and Ikeda attractors all possess regions dominated by decreasing uncertainties in time, where uncertainties associated with different trajectories issuing forth from some small neighborhood shrink for the amount of time trajectories remain within such regions (e.g., Smith, Ziehmann and Fraedrich 1999, pp. 2870–9; Ziehmann, Smith and Kurths 2000, pp. 273–83). Hence, on-average exponential growth in trajectory divergence is not guaranteed for chaotic dynamics. Linear stability analysis can indicate when nonlinearities can be expected to dominate the dynamics, and local finite-time Lyapunov exponents can indicate regions on an attractor where these nonlinearities will cause all uncertainties to decrease—cause trajectories to converge rather than diverge—so long as trajectories remain in those regions.
To summarize, the folklore that trajectories issuing forth from neighboring points will diverge on-average exponentially in a chaotic region of state space is false in any sense other than for infinitesimal uncertainties in the infinite time limit for simple mathematical models.
The second problem with the standard account is that there simply is no implication that finite uncertainties will exhibit an on-average growth rate characterized by any Lyapunov exponents, local or global. For example, the linearized dynamics used to derive global Lyapunov exponents presupposes infinitesimal uncertainties (Appendix (A1)–(A5)). But when uncertainties are finite, such dynamics do not apply and no valid conclusions can be drawn about the dynamics of finite uncertainties from the dynamics of infinitesimal uncertainties. Certainly infinitesimal uncertainties never become finite in finite time (barring super exponential growth). Even if infinitesimal uncertainties became finite after a finite time, that would presuppose the dynamics is unconfined, whereas the interesting features of nonlinear dynamics usually take place in subregions of state space. Presupposing an unconfined dynamics would be inconsistent with the features we are typically trying to capture.
Can the on average exponential growth rate characterizing SD ever be attributed legitimately to diverging trajectories if their separation is no longer infinitesimal? Examining simple models (e.g., the Baker's transformation) might seem to indicate yes. However, answering this question requires some care for more complex systems like the Lorenz or Moore-Spiegel attractors. It may turn out that the rate of divergence in the finite separation between two nearby trajectories in a chaotic region changes character numerous times over the course of their winding around in state space, sometimes faster, sometimes slower than that calculated from global Lyapunov exponents, sometimes contracting, sometimes diverging (Smith, Ziehmann and Fraedrich 1999; Ziehmann, Smith and Kurths 2000). But in the long run, some of these trajectories could effectively diverge as if there was on-average exponential growth in uncertainties as characterized by global Lyapunov exponents. However, it is conjectured that the set of initial points in the state space exhibiting this behavior is a set of measure zero, meaning, in this context, that although there are an infinite number of points exhibiting this behavior, this set represents zero percent of the number of points composing the attractor. The details of the kinds of divergence (convergence) neighboring trajectories undergo turn on the detailed structure of the dynamics (i.e., it is determined point-by-point by local growth and convergence of finite uncertainties and not by any Lyapunov exponents).
But as a practical matter, all finite uncertainties saturate at the diameter of the attractor. This is to say, that the uncertainty reaches some maximum amount of spreading after a finite time and is not well quantified by global measures derived from Lyapunov exponents (e.g., Lorenz 1965). So the folklore—that on-average exponential divergence of trajectories characterizes chaotic dynamics—is misleading for nonlinear models and systems, in particular the ones we want to label as chaotic. Therefore, drawing an inference from the presence of positive global Lyapunov exponents to the existence of on-average exponentially diverging trajectories is invalid. This has implications for defining chaos because exponential growth parametrized by global Lyapunov exponents turns out not to be an appropriate measure. Hence, SD or Chaos\(_{\lambda}\) turn out to be misleading definitions of chaos.
Finally, I want to briefly draw attention to the observer-dependent nature of global Lyapunov exponents in the special theory of relativity. As has been recently demonstrated (Zheng, Misra and Atmanspacher 2003), global Lyapunov exponents change in magnitude under Lorentz transformations, though not in sign—e.g., positive Lyapunov exponents are always positive under Lorentz transformations. Moreover, under Rindler transformations, global Lyapunov exponents are not invariant so that a system characterized as chaotic under SD or Chaos\(_{\lambda}\) for an accelerated Rindler observer turns out to be nonchaotic for an inertial Minkowski observer and any system that is chaotic for a an inertial Minkowski observer is nonchaotic for an accelerated Rindler observer. So along with the simultaneity subtleties raised for observers by Einstein's theory of special relativity (see the entry on conventionality of simultaneity), chaos, at least under SD or Chaos\(_{\lambda}\), turns out to also have observer-dependent features for pairs of observers in different reference frames. What these features mean for our understanding of the phenomenon of chaos remains largely unexplored.
1.2.7 Taking Stock
There is no consensus regarding a precise definition of chaotic behavior among mathematicians and physicists, although physicists often prefer Chaos\(_{h}\) or Chaos\(_{\lambda}\). The latter definitions, however, are trivially false for finite uncertainties in real systems and of limited applicability for mathematical models. It also appears to be the case that there is no one "right" or "correct" definition, but that varying definitions have varying strengths and weaknesses regarding tradeoffs on generality, theorem-generation, calculation ease and so forth. The best candidates for necessary conditions for chaos still appear to be (1) WSD, which is rather weak, or (2) the presence of stretching and folding mechanisms ("pulls trajectories apart" in one dimension while "compressing them" in another).
The other worry is that the definitions we have been considering may only hold for our mathematical models, but may not be applicable to actual target systems. The formal definitions seek to fully characterize chaotic behavior in mathematical models, but we are also interested in capturing chaotic behavior in physical and biological systems as well. Phenomenologically, the kinds of chaotic behaviors we see in actual-world systems exhibit features such as SDIC, aperiodicity, unpredictability, instability under small perturbations and apparent randomness. However, given that target systems run for only a finite amount of time and that the uncertainties are always larger than infinitesimal, such systems violate the assumptions necessary for deriving SD. In other words, even if we have good statistical measures that yield on average exponential growth in uncertainties for a physical data set, what guarantee do we have that this corresponds with the exponential growth of SD? After all, any growth in uncertainties (alternatively, any growth in distance between neighboring trajectories) can be fitted with an exponential. If there is no physical significance to global Lyapunov exponents (because they only apply to infinitesimal uncertainties), then one is free to choose any parameter to fit an exponential for the growth in uncertainties.
So where does this leave us regarding a definition of chaos? Are all our attempts at definitions inadequate? Is there only one definition for chaos, and if so, is it only a mathematical property or also a physical one? Do we, perhaps, need multiple definitions (some of which are nonequivalent) to adequately characterize such complex and intricate behavior? Is it reasonable to expect that the phenomenological features of chaos of interest to physicists and applied mathematicians can be captured in precise mathematical definitions given that there may be irreducible vagueness in the characterization of these features? From a physical point of view, isn't a phenomenological characterization sufficient for the purpose of identifying and exploring the underlying mechanisms responsible for the stretching and folding of trajectories? The answers to these questions largely lie in our purposes for the kinds of inquiry in which we are engaged (e.g., proving rigorous mathematical theorems vs. detecting chaotic behavior in physical data vs. designing systems to control such behavior).
Sitting in the background for all of these discussions is nonlinearity. Chaos only exists in nonlinear systems (at least for classical macroscopic systems; see sec. 6 for subtitles regarding quantum chaos). Nonlinearity appears to be a necessary condition for the stretching and folding mechanisms, so would seem to be a necessary condition for chaotic behavior. However, there is an alternative way to characterize the systems in which such stretching and folding takes place: nonseparability.
As discussed in Section 1.2.2, linear systems always obey the principle of linear superposition. This implies that the Hamiltonians for such systems are always separable. A separable Hamiltonian can always be transformed into a sum of separate Hamiltonians with one element in the sum corresponding to each subsystem. In effect, a separable system is one where the interactions among subsystems can be transformed away leaving the subsystems independent of each other. The whole is the sum of the parts, as it were. Chaos is impossible for separable Hamiltonians. For a nonlinear systems, by contrast, Hamiltonians are never separable. There are no transformation techniques that can turn a nonseparable Hamiltonian into the sum of separate Hamiltonians. In other words, the interactions in a nonlinear system cannot be decomposed into individual independent subsystems, nor can the whole system and its environment be ignored (Bishop 2010a). Nonseparable classical systems are the kinds of systems where chaotic behavior can manifest itself. So alternatively one could say that nonseparability of a Hamiltonian is a necessary condition for stretching and folding mechanisms and, hence, for chaos (e.g., Kronz 1998).
2. What is Chaos "Theory"?
One often finds references in the literature to "chaos theory." For instance, Kellert characterizes chaos theory as "the qualitative study of unstable aperiodic behavior in deterministic nonlinear systems" (Kellert 1993, p. 2). In what sense is chaos a theory? Is it a theory in the same sense that electrodynamics or quantum mechanics are theories?
Answering such questions is difficult if for no other reason than that there is no consensus about what a theory is. Scientists often treat theories as systematic bodies of knowledge that provide explanations and predictions for actual-world phenomena. But trying to get more specific or precise than this generates significant differences for how to conceptualize theories. Options here range from the axiomatic or syntactic view of the logical positivists and empiricists (see Vienna Circle) to the semantic or model-theoretic view (see models in science), to Kuhnian (see Thomas Kuhn) and less rigorous conceptions of theories. The axiomatic view of theories appears to be inapplicable to chaos. There are no axioms—no laws—no deductive structures, no linking of observational statements to theoretical statements whatsoever in the literature on chaotic dynamics.
Kellert's (1993) focus on chaos models is suggestive of the semantic view of theories, and many texts and articles on chaos focus on models (e.g., logistic map, Henon map, Lorenz attractor). Briefly, on the semantic view, a theory is characterized by (1) some set of models and (2) the hypotheses linking these models with idealized physical systems. The mathematical models discussed in the literature are concrete and fairly well understood, but what about the hypotheses linking chaos models with idealized physical systems? In the chaos literature, there is a great deal of discussion of various robust or universal patterns and the kinds of predictions that can and cannot be made using chaotic models. Moreover, there is a lot of emphasis on qualitative predictions, geometric "mechanisms" and patterns, but this all comes up short of spelling out hypotheses linking chaos models with idealized physical systems.
One possibility is to look for hypotheses about how such models are deployed when studying actual physical systems. Chaos models seem to be deployed to ascertain various kinds of information about bifurcation points, period doubling sequences, the onset of chaotic dynamics, strange attractors and other denizens of the chaos zoo of behaviors. The hypotheses connecting chaos models to physical systems would have to be filled in if we are to employ the semantic conception fully. I take it these would be hypotheses about, for example, how strange attractors reconstructed from physical data relate to the physical system from which the data were originally recorded. Or about how a one-dimensional map for a particular full nonlinear model (idealized physical system) developed using, say, Poincaré surface of section techniques, relates to the target system being modeled.
Such an approach does seem consistent with the semantic view as illustrated with classical mechanics. There we have various models such as the harmonic oscillator and hypotheses about how these models apply to idealized physical systems, including specifications of spring constants and their identification with mathematical terms in a model, small oscillation limits, and so forth. But in classical mechanics there is a clear association between the models of a theory and the state spaces definable over the variables of those models, with a further hypothesis about the relationship between the model state space and that of the physical system being modeled (the faithful model assumption, §1.2.3). One can translate between the state spaces and the models and, in the case of classical mechanics, can read the laws off as well (e.g., Newton's laws of motion are encoded in the possibilities allowed in the state spaces of classical mechanics).
Unfortunately, the connection between state spaces, chaotic models and laws is less clear. Indeed, there currently are no good candidates for laws of chaos over and above the laws of classical mechanics, and some, such as Kellert, explicitly deny that chaos modeling is getting at laws at all (1993, ch. 4). Furthermore, the relationship between the state spaces of chaotic models and the spaces of idealized physical systems is quite delicate, which seems to be a dissimilarity between classical mechanics and "chaos theory." In the former case, we seem to be able to translate between models and state spaces.[3] In the latter, we can derive a state space for chaotic models from the full nonlinear model, but we cannot reverse the process and get back to the nonlinear model state space from that of the chaotic model. One might expect the hypotheses connecting chaos models with idealized physical systems to piggy back on the hypotheses connecting classical mechanics models with their corresponding idealized physical systems. But it is neither clear how this would work in the case of nonlinear systems in classical mechanics, nor how this would work for chaotic models in biology, economics and other disciplines.[4]
Additionally, there is another potential problem that arises from thinking about the faithful model assumption, namely what is the relationship or mapping between model and target system? Is it one-to-one as we standardly assume? Or is it a one-to-many relation (several different nonlinear models of the same target system or, potentially, vice versa) or a many-to-many relationship?[5] For many classical mechanics problems—namely, where linear models or force functions are used in Newton's second law—the mapping or translation between model and target system appears to be straightforwardly one-to-one. However, in nonlinear contexts, where one might be constructing a model from a data set generated by observing a system, there are potentially many nonlinear models that can be constructed, where each model is as empirically adequate to the system behavior as any other. Is there really only one unique model for each target system and we simply do not know which is the "true" one (say, because of underdeterminiation problems—see scientific realism)? Or is there really no one-to-one relationship between our mathematical models and target systems?
Moreover, an important feature of the semantic view is that models are only intended to capture the crucial features of target systems and always involve various forms of abstraction and idealization (see models in science). These caveats are potentially deadly in the context of nonlinear dynamics. Any errors in our models for such systems, no matter how accurate our initial data, will lead to errors in predicting actual systems as these errors will grow (perhaps rapidly) with time. This brings out one of the problems with the faithful model assumption that is hidden, so to speak, in the context of linear systems. In the latter context, models can be erroneous by leaving out "negligible" factors and, at least for reasonable times, our model predictions do not differ significantly with the target systems we are modeling (wait long enough, however, and such predictions will differ significantly). In nonlinear contexts, by contrast, it is not so clear there are any "negligible" factors. Even the smallest omission in a nonlinear model can lead to disastrous effects because the differences these terms would have made versus their absence potentially can be rapidly amplified as the model evolves (see §3).
Another possibility is to drop hypotheses connecting models with target systems and simply focus on the defining models of the semantic view of theories. This is very much the spirit of the mathematical theory of dynamical systems. There the focus is on models and their relations, but there is no emphasis on hypotheses connecting these models with actual systems, idealized or otherwise. Unfortunately, this would mean that chaos theory would be only a mathematical theory and not a physical one.
Both the syntactic and semantic views of theories focus on the formal structure of theoretical bodies, and their "fit" with theorizing about chaotic dynamics seems quite problematic. In contrast, perhaps one should conceive of chaos theory in a more informal or paradigmatic way, say along the lines of Kuhn's (1996) analysis of scientific paradigms. There is no emphasis on the precise structure of scientific theories in Kuhn's picture of science. Rather, theories are cohesive, systematic bodies of knowledge defined mainly by the roles they play in normal science practice within a dominant paradigm. There is a very strong sense in literature about chaos that a "new paradigm" has emerged out of chaos research with its emphasis on unstable rather than stable behavior, on dynamical patterns rather than on mechanisms, on universal features (e.g., Feigenbaum's number) rather than laws, and on qualitative understanding rather than on precise prediction. Whether or not chaotic dynamics represents a genuine scientific paradigm, the use of the term 'chaos theory' in much of the scientific and philosophical literature has the definite flavor of characterizing and understanding complex behavior rather than an emphasis on the formal structure of principles and hypotheses.
3. Nonlinear Models, Faithfulness and Confirmation
Given a target system to be modeled, and invoking the faithful model assumption, there are two basic approaches to model confirmation discussed in the philosophical literature on modeling following a strategy known as piecemeal improvement (I will ignore bootstrapping approaches as they suffer similar problems, but only complicate the discussion). These piecemeal strategies are also found in the work of scientists modeling actual-world systems and represent competing approaches vying for government funding (for an early discussion, see Thompson 1957).
The first basic approach is to focus on successive refinements to the accuracy of the initial data used by the model while keeping the model itself fixed (e.g., Laymon 1989, p. 359). The idea here is that if a model is faithful in reproducing the behavior of the target system to some degree, refining the precision of the initial data fed to the model will lead to its behavior monotonically converging to the target system's behavior. This is to say that as the uncertainty in the initial data is reduced, a faithful model's behavior is expected to converge to the target system's behavior. The import of the faithful model assumption is that if one were to plot the trajectory of the target system in an appropriate state space, the model trajectory in the same state space would monotonically become more like the system trajectory on some measure as the data is refined (I will ignore difficulties regarding appropriate measures for discerning similarity in trajectories; see Smith 2000).
The second basic approach is to focus on successive refinements of the model while keeping the initial data fixed (e.g., Wimsatt 1987). The idea here is that if a model is faithful in reproducing the behavior of the target system, refining the model will produce an even better fit with the target system's behavior. This is to say that if a model is faithful, successive improvements will lead to its behavior monotonically converging to the target system's behavior. Again, the import of the faithful model assumption is that if one were to plot the trajectory of the target system in an appropriate state space, the model trajectory in the same state space would monotonically become more like the system trajectory as the model is made more realistic.
What both of these basic approaches have in common is that piecemeal monotonic convergence of model behavior to target system behavior is a mark for confirmation of the model (Koperski 1998). By either improving the quality of the initial data or improving the quality of the model, the model in question reproduces the target system's behavior monotonically better and yields predictions of the future states of the target system that show monotonically less deviation with respect to the behavior of the target system. In this sense, monotonic convergence to the behavior of the target system is a key criterion for whether the model is confirmed. If monotonic convergence to the target system behavior is not found by pursuing either of these basic approaches, then the model is considered to be disconfirmed.
For linear models it is easy to see the intuitive appeal of such piecemeal strategies. After all, for linear systems of equations a small change in the magnitude of a variable is guaranteed to yield a proportional change in the output of the model. So by making piecemeal refinements to the initial data or to the linear model only proportional changes in model output are expected. If the linear model is faithful, then making small improvements "in the right direction" in either the initial data or the model itself can be tracked by improved model performance. The qualifier "in the right direction," drawing upon the faithful model assumption, means that the data quality really is increased or that the model really is more realistic (captures more features of the target system in an increasingly accurate way), and is signified by the model's monotonically improved performance with respect to the target system.
However, both of these basic approaches to confirming models encounter serious difficulties when applied to nonlinear models, where the principle of linear superposition no longer holds. In the first approach, successive small refinements in the initial data used by nonlinear models is not guaranteed to lead to any convergence between model behavior and target system behavior. Any small refinements in initial data can lead to non-proportional changes in model behavior rendering this piecemeal convergence strategy ineffective as a means for confirming the model. A refinement of the quality of the data "in the right direction" is not guaranteed to lead to a nonlinear model monotonically improving in capturing the target system's behavior. The small refinement in data quality may very well lead to the model behavior diverging away from the system's behavior.[6]
In the second approach, keeping the data fixed but making successive refinements in nonlinear models is also not guaranteed to lead to any convergence between model behavior and target system behavior. With the loss of linear superposition, any small changes in the model can lead to non-proportional changes in model behavior again rendering the convergence strategy ineffective as a means for confirming the model. Even if a small refinement to the model is made "in the right direction," there is no guarantee that the nonlinear model will monotonically improve in capturing the target system's behavior. The small refinement in the model may very well lead to the model behavior diverging away from the system's behavior.
So whereas for linear models piecemeal strategies might be expected to lead to better confirmed models (presuming the target system exhibits only stable linear behavior), no such expectation is justified for nonlinear models deployed in the characterization of nonlinear target systems. Even for a faithful nonlinear model, the smallest changes in either the initial data or the model itself may result in non-proportional changes in model output, an output that is not guaranteed to "move in the right direction" even if the small changes are made "in the right direction" (of course, this lack of guarantee of monotonic improvement also raises questions about what "in the right direction" means, but I will ignore these difficulties here).
Intuitively, piecemeal convergence strategies look to be dependent on the perfect model scenario. Given a perfect model, refining the quality of the data should lead to monotonic convergence of the model behavior to the target system's behavior, but even this expectation is not always justifiable for perfect models (cf. Judd and Smith 2001; Smith 2003). On the other hand, given good data, perfecting a model intuitively should also lead to monotonic convergence of the model behavior to the target system's behavior. By making small changes to a nonlinear model, hopefully based on improved understanding of relevant features of the target system (e.g., the physics of weather systems or the structures of economies), there is no guarantee that such changes will produce monotonic improvement in the model's performance with respect to the target system's behavior. The loss of linear superposition, then, leads to a similar lack of guarantee of a continuous path of improvement as the lack of guarantee of piecemeal confirmation. And without such a guaranteed path of improvement, there is no guarantee that a faithful nonlinear model can be perfected by piecemeal means.
Of course, we do not have perfect models. But even if we did, they are unlikely to live up to our intuitions about them (Judd and Smith 2001; Judd and Smith 2004). For example, no matter how many observations of a system are made, there still will be a set of trajectories in the model state space that are indistinguishable from the actual trajectory of the target system. Indeed, even for infinite past observations, we cannot eliminate the uncertainty in the epistemic states given some unknown ontological state of the target system. One important reason for this difficulty follows from the faithful model assumption. Suppose the nonlinear model state space is a faithful representation of the possibilities lying in the physical space of the target system. No matter how fine-grained we make our model state space, it will still be the case that there are many different states of the actual target system (ontological states) that are mappable into the same state of the model state space (epistemic states). This means that there will always be many more target system states than there are model states for any computational models since the equations have to be discretized. In principle, in those cases where we can develop a fully analytical model, we could get an exact match between the number of possible model states and the number of target system states. However, such analytical models are rare in complexity studies (many of the analytical models are toy models, like the baker's map, which, while illustrative of techniques, are misleading when it comes to metaphysical and ontological conclusions due to their simplicity).
Therefore, whether there is a perfect model or not for a target system, there is no guarantee of monotonic improvement with respect to the target system's behavior. Traditional piecemeal confirmation strategies fail. This is the upshot of the failure of the principle of linear superposition. No matter how faithful the model, no guarantee of piecemeal monotonic improvement of a nonlinear model's behavior with respect to the target system can be made (of course, if one waits for long enough times piecemeal confirmation strategies will also fail for linear systems). Furthermore, problems with these confirmation strategies will arise whether one is seeking to model point-valued trajectories in state space or one is using probability densities defined on state space.
One possible response to the piecemeal confirmation problems discussed here is to turn to a Bayesian framework for confirmation, but similar problems arise here for nonlinear models. Given that there are no perfect models in the model class to which we would apply a Bayesian scheme and given the fact that imperfect models will fail to reproduce or predict target system behavior over time scales that may be short compared to our interests, there again is no guarantee that monotonic improvement can be achieved for our nonlinear models (I leave aside the problem that having no perfect model in our model class renders many Bayesian confirmation schemes ill-defined).
For nonlinear models, faithfulness can fail and piecemeal perfectibility cannot be guaranteed, raising questions about scientific modeling practices and our understanding of them. However, the implications of the loss of linear superposition reach father than this. Policy assessment often utilizes model forecasts and if the models and systems lying at the core of policy deliberations are nonlinear, then policy assessment will be affected by the same lack of guarantee as model confirmation. Suppose administrators are using a nonlinear model in the formulation of economic policies designed to keep GDP ever increasing while minimizing unemployment (among achieving other socio-economic goals). While it is true that there will be some uncertainty generated by running the model several times over slightly different data sets, assume that policies taking these uncertainties into account to some degree can be fashioned. Once in place, the policies need assessment regarding their effectiveness and potential adverse effects, but such assessment will not involve merely looking at monthly or quarterly reports on GDP and employment data to see if targets are being met. The nonlinear economic model driving the policy decisions will need to be rerun to check if trends are indeed moving "in the right direction" with respect to the earlier forecasts. But, of course, data for the model now has changed and there is no guarantee that the model will produce a forecast with this new data that fits well with the old forecasts used to craft the original policies. Nor is there a guarantee of any fit between the new runs of the nonlinear model and the economic data being gathered as part of ongoing monitoring of the economic policies. How, then, are policy makers to make reliable assessments of policies? The same problem—that small changes in data or model in nonlinear contexts are not guaranteed to yield proportionate model outputs or monotonically improved model performance—also plagues policy assessment using nonlinear models. Such problems remain largely unexplored.
4. Chaos, Determinism and Quantum Mechanics
One of the exciting features of SDIC is that there is no lower limit on just how small some change or perturbation can be—the smallest of effects will eventually be amplified up affecting the behavior of any system exhibiting SDIC. A number of authors have argued that chaos through SDIC opens a door for quantum mechanics to "infect" chaotic classical mechanics systems (e.g., Hobbs 1991; Barone et al. 1993; Kellert 1993; Bishop 2008). [7] The essential point is that the nature of particular kinds of nonlinear dynamics—those which exhibit stretching and folding (confinement) of trajectories, where there are no trajectory crossings, and which exhibit aperiodic orbits—apparently open the door for quantum effects to change the behavior of chaotic macroscopic systems. The central argument runs as follows and is known as the sensitive dependence argument (SD argument for short):
- For systems exhibiting SDIC, trajectories starting out in a highly localized region of state space will diverge on-average exponentially fast from one another.
- Quantum mechanics limits the precision with which physical systems can be specified to a neighborhood in phase space of no less than \(1/(2\pi/h)^{N}\), where \(h\) is Plank's constant (with units of action) and \(N\) is the dimension of the system in question.
- Given enough time and the quantum mechanical bound on the neighborhood \(\varepsilon\) for the initial conditions, two trajectories of the same chaotic system will have future states localizable to a much larger region \(\delta\) in phase space (from (A) and (B)).
- Therefore, quantum mechanics will influence the outcomes of chaotic systems leading to a violation of unique evolution.
Premise (A) makes clear that SD is the operative definition for characterizing chaotic behavior in this argument, invoking exponential growth characterized by the largest global Lyapunov exponent. Premise (B) expresses the precision limit for the state of minimum uncertainty for momentum and position pairs in an \(N\)-dimensional quantum system (note, the exponent is \(2N\) in the case of uncorrelated electrons).[8] The conclusion of the argument in the form given here is actually stronger than that quantum mechanics can influence a macroscopic system exhibiting SDIC; determinism fails for such systems because of such influences. Briefly, the reasoning runs as follows. Because of SDIC, nonlinear chaotic systems whose initial states can be located only within a small neighborhood \(\varepsilon\) of state space will have future states that can be located only within a much larger patch \(\delta\). For example, two isomorphic nonlinear systems of classical mechanics exhibiting SDIC, whose initial states are localized within \(\varepsilon\), will have future states that can be localized only within \(\delta\). Since quantum mechanics sets a lower bound on the size of the patch of initial conditions, unique evolution must fail for nonlinear chaotic systems.
The SD argument does not go through as smoothly as some of its advocates have thought, however. There are difficult issues regarding the appropriate version of quantum mechanics (e.g., von Neumann, Bohmian or decoherence theories; see entries under quantum mechanics), the nature of quantum measurement theory (collapse vs. non-collapse theories; see the section on the measurement problem in the entry on philosophical issues in quantum theory), and the selection of the initial state characterizing the system that must be resolved before one can say clearly whether or not unique evolution is violated. For instance, just because quantum effects might influence macroscopic chaotic systems doesn't guarantee that determinism fails for such systems. Whether quantum interactions with nonlinear macroscopic systems exhibiting SDIC contribute indeterministically to the outcomes of such systems depends on the currently undecidable question of indeterminism in quantum mechanics and the measurement problem as well as on how one chooses to the system-measurement apparatus cut (Bishop 2008).
To expand on one issue, there is a serious open question as to whether the indeterminism in quantum mechanics is simply the result of ignorance due to epistemic limitations or if it is an ontological feature of the quantum world. Suppose that quantum mechanics is ultimately deterministic, but that there is some additional factor, a hidden variable as it is often called, such that if this variable were available to us, our description of quantum systems would be fully deterministic. Another possibility is that there is an interaction with the broader environment that accounts for how the probabilities in quantum mechanics arise (physicists call this approach "decoherence"). Under either of these possibilities, we would interpret the indeterminism observed in quantum mechanics as an expression of our ignorance, and, hence, indeterminism would not be a fundamental feature of the quantum domain. It would be merely epistemic in nature due to our lack of knowledge or access to quantum systems. So if the indeterminism in QM is not ontologically genuine, then whatever contribution quantum effects make to macroscopic systems exhibiting SDIC would not violate unique evolution. In contrast, suppose it is the case that quantum mechanics is genuinely indeterministic; that is, all the relevant factors of quantum systems do not fully determine their behavior at any given moment. Then the possibility exists that not all physical systems traditionally thought to be in the domain of classical mechanics can be described using strictly deterministic models, leading to the need to approach the modeling of such nonlinear systems differently.
Moreover, the possible constraints of nonlinear classical mechanics systems on the amplification of quantum effects must be considered on a case-by-case basis. For instance, damping due to friction can place constraints on how quickly amplification of quantum effects can take place before they are completely washed out (Bishop 2008). And one has to investigate the local finite-time dynamics for each system because these may not yield any on-average growth in uncertainties (e.g., Smith, Ziehmann, Fraedrich 1999).
In summary, there is no abstract, a priori reasoning establishing the truth of the SD argument; the argument can only be demonstrated on a case-by-case basis. Perhaps detailed examination of several cases would enable us to make some generalizations about how wide spread the possibilities for the amplification of quantum effects are.
5. Questions about Realism and Explanation
Two traditional topics in philosophy of science are realism and explanation. Although not well explored in the context of chaos, there are interesting questions regarding both topics deserving of further exploration.
5.1 Realism and Chaos
Chaos raises a number of questions about scientific realism (see scientific realism) only some of which will be touched on here. First and foremost, scientific realism is usually formulated as a thesis about the status of unobservable terms in scientific theories and their relationship to entities, events and processes in the actual world. In other words, theories make various claims about features of the world and these claims are at least approximately true. But as we saw in §2, there are serious questions about formulating a theory of chaos, let alone determining how this theory fares under scientific realism. It seems more reasonable, then, to discuss some less ambitious realist questions regarding chaos: Is chaos an actual phenomenon? Do the various denizens of chaos, like fractals, actually exist?
This leads us back to the faithful model assumption (§1.2.3). Recall this assumption maintains that our model equations faithfully capture target system behavior and that the model state space faithfully represents the actual possibilities of the target system. Is the sense of faithfulness here that of actual correspondence between mathematical models and features of actual systems? Or can faithfulness be understood in terms of empirical adequacy alone, a primarily instrumentalist construal of faithfulness? Is a realist construal of faithfulness threatened by the mapping between models and systems potentially being one-to-many or many-to-many?
A related question is whether or not our mathematical models are simulating target systems or merely mimicking their behavior. To be simulating a system suggests that there is some actual correspondence between the model and the target system it is designed to capture. On the other hand, if a mathematical model is merely mimicking the behavior of a target system, there is no guarantee that the model has any genuine correspondence to the actual properties of the target system. The model merely imitates behavior. These issues become crucial for modern techniques of building nonlinear dynamical models from large time series data sets (e.g., Smith 1992), for example the sunspot record or the daily closing value of a particular stock for some specific period of time. In such cases, after performing some tests on the data set, the modeler sets to work constructing a mathematical model that reproduces the time series as its output. Do such models only mimic behavior of target systems? Where does realism come into the picture?
A further question regarding chaos and realism is the following: Is chaos only a feature of our mathematical models or is it a genuine feature of actual systems in our world? This question is well illustrated by a peculiar geometric structure of dissipative chaotic models called a strange attractor, which can form based upon the stretching and folding of trajectories in state space. Strange attractors normally only occupy a subregion of state space, but once a trajectory wanders close enough to the attractor, it is caught near the surface of the attractor for the rest of its future.
One of the characteristic features of strange attractors is that they posses self-similar structure. Magnify any small portion of the attractor and you would find that the magnified portion would look identical to the regular-sized region. Magnify the magnified region and you would see the identical structure repeated again. Continuous repetition of this process would yield the same results. The self-similar structure is repeated on arbitrarily small scales. An important geometric implication of self-similarity is that there is no inherent size scale so that we can take as large a magnification of as small a region of the attractor as we want and a statistically similarly structure will be repeated (Hilborn 1994, p. 56). In other words, strange attractors for chaotic models have an infinite number of layers of repetitive structure. This type of structure allows trajectories to remain within a bounded region of state space by folding and intertwining with one another without ever intersecting or repeating themselves exactly.
Strange attractors also are often characterized as possess noninteger or fractal dimension (though not all strange attractors have such dimensionality). The type of dimensionality we usually meet in physics as well as in everyday experience is characterized by integers. A point has dimension zero; a line has dimension one; a square has dimension two; a cube has dimension three and so on. As a generalization of our intuitions regarding dimensionality, consider a large square. Suppose we fill this large square with smaller squares each having an edge length of \(\varepsilon\). The number of small squares needed to completely fill the space inside the large square is \(N(\varepsilon)\). Now repeat this process of filling the large square with small squares, but each time let the length \(\varepsilon\) get smaller and smaller. In the limit as \(\varepsilon\) approached zero, we would find that the ratio \(\ln N(\varepsilon)/\ln(1 / \varepsilon)\) equals two just as we would expect for a 2-dimensional square. You can imagine the same exercise of filling a large 3-dimensional cube (a room, say) with smaller cubes and in the limit of \(\varepsilon\) approaching zero, we would arrive at a dimension of three.
When we apply this generalization of dimensionality to the geometric structure of strange attractors, we often find noninteger dimensionality. Roughly this means that if we try to apply the same procedure of "filling" the structure formed by the strange attractor with small squares or cubes, in the limit as \(\varepsilon\) approaches zero the result is noninteger. Whether one is examining a set of nonlinear mathematical equations or analyzing the time series data from an experiment, the presence of self-similarity or noninteger dimension are indications that the chaotic behavior of the system under study is dissipative (nonconservative, doesn't conserve energy) rather than Hamiltonian (does conservative energy).
Although there is no universally accepted definition for strange attractors or fractal dimension among mathematicians, the more serious question is whether strange attractors and fractal dimensions are properties of our models only or also of actual-world systems. For instance, empirical investigations of a number of actual-world systems indicate that there is no infinitely repeating self-similar structure like that of strange attractors (Avnir, et al. 1998; see also Shenker 1994). At most, one finds self-similar structure repeated on two or three spatial scales in the reconstructed state space and that is it. This appears to be more like a prefractal, where self-similar structure exists on only a finite number of length scales. That is to say, prefractals repeat their structure under magnification only a finite number of times rather than infinitely as in the case of a fractal. So this seems to indicate that there are no genuine strange attractors with fractal dimension in actual systems, but possibly only attractors having prefractal geometries with self-similarity on a limited number of spatial scales.
On the other hand, the dissipative chaotic models used to characterize some actual-world systems all exhibit strange attractors with fractal geometries. So it looks like fractal geometries in chaotic model state spaces bear no relationship to the pre-fractal features of actual-world systems. In other words, these fractal features of many of our models are clearly false of the target systems though the models themselves may still be useful for helping scientists locate interesting dynamics of target systems characterized by prefractal properties. Scientific realism and usefulness look to part ways here. At least many of the strange attractors of our models play the role of useful fictions.
There are caveats to this line of thinking, however. First, the prefractal character of the analyzed data sets (e.g. by Avnir, et al. 1998) could be an artifact of the way data is massaged before it is analyzed or due to the analog-to-digital conversion that must take place before data analysis can begin. Reducing real number valued data to a finite string of would destroy fractal structure. If so, the infinitely self-similar structures of fractals in our models might not be such a bad approximation after all.
A different reason, though, to suspect that physical systems cannot have such self-repeating structures "all the way down" is that at some point the classical world gives way to the quantum world, where things change so drastically that there cannot be a strange attractor because the state space changes. Hence, we are applying a model carrying a tremendous amount of excess, fictitious structure to understand features of physical systems. This looks like a problem because one of the key structures playing a crucial role in chaos explanations—the infinitely intricate structure of the strange attractor—would then be absent from the corresponding physical system.
According to Peter Smith (1998, ch. 3), one might be justified in employing obviously false chaos models because the infinitely intricate structure of strange attractors (1) is the result of relatively simple stretching and folding mechanisms and (2) many of the points in state space of interest are invariant under this stretching and folding mechanism. These features represent kinds of simplicity that can be had at the (perhaps exorbitant!) cost of fictitious infinite structure. The strange attractor exhibits this structure and the attractor is a sign of some stretching and folding process. The infinite structure is merely geometric extra baggage, but the robust properties like period-doubling sequences, onset of chaos, and so forth are real enough. This has the definite flavor of being antirealist about some key elements of explanation in chaos (§5.2) and has been criticized as such (Koperski 2001).
Instead of trying to squeeze chaos into scientific realism's mold, then, perhaps it is better to turn to an alternative account of realism, structural realism. Roughly, the idea is that realism in scientific practices hinges on the structural relations of phenomena. So structural realism tends to focus on the causal structures in well-confirmed scientific hypotheses and theories. The kinds of universal structural features identified in chaotic phenomena in realms as diverse as physics, biology and economics is very suggestive of some form of structural realism and, indeed, look to play key roles in chaos explanations (see below). Though, again, there are significant worries that infinitely repeating self-similar structure might not be realized in physical systems. On a structural approach to realism regarding chaos models, one faces the difficulty that strange attractors are at best too gross an approximation to the structure of physical attractors and at worst terribly misleading.
Perhaps other kinds of geometric structures associated with chaos would qualify on a structural realist view. After all, it also seems to be the case that realism for chaos models has more to do with processes—namely stretching and folding mechanisms at work in target systems. But here the connection with realism and chaos models would come indirectly via an appeal to the causal processes at work in the full nonlinear models taken to represent physical systems. Perhaps the fractal character of strange attractors is an artifact introduced through the various idealizations and approximations used to derive such chaotic models. If so, then perhaps there is another way to arrive at more realistic chaos models that have prefractal attractors.
5.2 The Nature of Chaos Explanations
Chaos has been invoked as an explanation for, or as contributing substantially to explanations of, actual-world behaviors. Some examples are epileptic seizures, heart fibrillation, neural processes, chemical reactions, weather, industrial control processes and even forms of message encryption. Aside from irregular behavior of actual-world systems, chaos is also invoked to explain features such as the actual trajectories exhibited in a given state space or the sojourn times of trajectories in particular regions of state space. But what, exactly, is the role chaos plays in these various explanations? More succinctly, what are chaos explanations?
The nature of scientific explanation (see the entry on scientific explanation) in the literature on chaos is thoroughly under-discussed to put it mildly. Traditional accounts for scientific explanation such as covering-law, causal mechanical and unification models all present various kinds of drawbacks when applied to chaotic phenomena. For instance, if there are no universal laws lying at the heart of chaos explanations—and it does not seem credible that such laws could really play a role in chaos explanations—covering-law models do not look promising as candidates for chaos explanations.
Roughly speaking, the causal-mechanical model of explanation maintains that science provides understanding of diverse facts and events by showing how these fit into the causal structure of the world. If chaos is a behavior exhibited by nonlinear systems (mathematical and physical), then it seems reasonable to think that there might be some mechanisms or processes standing behind this behavior. After all, chaos is typically understood to be a property of the dynamics of such systems, and dynamics often reflects the processes at work and their interactions. The links between causal mechanisms and behaviors in the causal-mechanical model are supposed to be reliable links along the following lines: If mechanism \(C\) is present, behavior \(B\) typically follows. In this sense, chaos explanations, understood on the causal-mechanical model, are envisioned as providing reliable connections between mechanisms and the chaotic behavior exhibited by systems containing such mechanisms.
On the other hand, the basic idea of unification accounts of explanation is that science provides understanding of diverse facts and events by showing how these may be unified by a much smaller set of factors (e.g., laws or causes). Perhaps one can argue that chaos is a domain or set of a limited number of patterns and tools for explaining/understanding a set of characteristic behaviors found in diverse phenomena spread across physics, chemistry, biology, economics, social psychology, and so forth. In this sense the set of patterns or structures (e.g., "stretching and folding") might make up the explanatory store unifying our understanding of all the diverse phenomena behaving chaotically.
5.2.1 Explanation, Faithful Models and Chaos
Both causal and unification accounts, as typically conceived, assume that theories are in place and that the models of those theories play some role in explanation. In causal accounts, causal processes are key components of the models. In unification accounts, laws might be the ultimate explanatory factors, but we often connect laws with physical systems via models. To be explanatory, however, such accounts must make the faithful model assumption; namely, that our models (and their state spaces) are faithful in what they say about actual systems.
Recall that SD—exponential divergence of neighboring trajectories—is taken by many to be a necessary condition for chaos. As we saw in §3, it is not straightforward to confirm when we have a model serving as a good explanation because, for instance, the slightest refinement of initial conditions can lead to wildly differing behavior. So on many standard approaches to confirmation and models, it would be difficult to say when we had a good explanation. Even if we push the faithful model assumption to its extreme limit—i.e., assuming the model is perfect—we run into tricky questions regarding confirmation since there are too many states indistinguishable from the actual state of the system yielding empirically indistinguishable trajectories in the model state space (Judd and Smith 2001).
Perhaps with chaos explanation we should either search for a process yielding the "stretching and folding" in the dynamics (causal form of explanation) or we should search for the common properties such behavior exhibits (unification form of explanation) underlying the behavior of the nonlinear systems of interest. In other words, we want to be able to understand why systems exhibit SDIC, aperiodicity, randomness, and so forth. But these are the properties characterizing chaotic behavior, so the unification account of explanation sounds like it may ultimately involve appealing to the properties in need of explanation.
The explanatory picture becomes more complicated by shifting away from SD as characterized by a positive global Lyapunov exponent and settling for what may be more realistic, namely the effects of divergence/contraction characterized by finite-time Lyapunov exponents. However, even in this case, it appears that the properties to which one appeals on a unification account pick out the patterns of chaos that we want to understand: How do these properties arise? It seems that unification accounts are still at a disadvantage in characterizing chaos explanations.
Suppose we appealed to strange attractors in our models or in state space reconstruction techniques. Would this be evidence that there is a strange attractor in the target system's behavior? Modulo worries raised in §5.1, even if the presence of a strange attractor in the state space was both a necessary and sufficient condition for the model being chaotic, this would not amount to an explanation of chaotic behavior in the target system. First, the strange attractor is an object in state space, which is not the same as saying that the actual system behaves as if there is a strange attractor in the physical space of its activity. A trajectory in a state space is a way of gaining useful information about the target system (via the faithful model assumption), but it is different from trajectories developed by looking at how an actual system's properties change with respect to time. Just because a trajectory of a system in state space is spiraling ever closer to the strange attractor does not imply that the target system's behavior in physical space is somehow approaching that attractor (except possibly under the perfect model scenario). Second, but related, the presence of a strange attractor would only be a mark of chaos, not an explanation for why chaotic properties are being exhibited by a system. It seems we still need to appeal to processes and interactions causing the dynamics to have the characteristic properties we associate with chaos.
At this point, a question implied at the end of the previous subsection arises, namely what is effecting the unification in chaos explanations? Unification models of explanation typically posit an explanatory store of a relatively small number of laws or mechanisms that serve to explain or unify a diverse set of phenomena. A standard example is that of Newtonian mechanics providing a small set of principles that could serve to explain phenomena as diverse as projectile motions, falling bodies, tides, planetary orbits and pendula. In this way, we say that Newtonian mechanics unified a diverse set of phenomena by showing that they all were governed by a small set of physical principles. Now, if a unification construal of chaos explanations only focuses on the mathematical similarities in behaviors of diverse phenomena (e.g., period doubling route to chaos or SDIC), then one can legitimately question whether the relevant sense of unification is in play in chaos explanations. The "explanatory store" of chaos explanations is indeed a small set of mathematical and geometrical features, but is this the wrong store (compare with the physical principles of Newtonian mechanics)? However, if unification is supposed to be achieved through underlying mechanisms producing these mathematical and geometrical features, then the explanatory store appears to be very large and heterogeneous—the mechanisms in physics are different from those in biology, are different from those in ecology, are different from those in economics are different from those in social psychology…Once again, the causal-mechanical model appears to make more sense for characterizing the nature of chaos explanations.
5.2.2 Chaos and Understanding
If this were all there was to the story of chaos explanations, then a causal account of explanation looks more promising. But it would also be the case that there is nothing special about such explanations: There are processes and interactions that cause the dynamics to have chaotic properties. But Stephen Kellert (1993, ch. 4) maintains that there is something new about chaotic dynamics, forcing us to rethink explanation when it comes to chaos models. His proposal for chaos explanations as yielding qualitative understanding of system behavior suggests that causal accounts, at least, do not fit well with what is going on in chaos research.
Kellert first focuses on one of the key intuitions driving many views in debates on scientific explanation: Namely, that the sciences provide understanding or insight into phenomena. Chaos explanations, according to Kellert, achieve understanding by constructing, elaborating and applying simple dynamical models. He gives three points of contrast between this approach to understanding and what he takes to be the standard approach to understanding in the sciences. The first is that chaos explanations involve models that are holistic rather than microreductionist. Models of the latter type seek to break systems down into their constituent parts and look for law-like relations among the parts. In contrast, many of the mathematical tools of chaotic dynamics are holistic in that they extract or reveal information about the behavior of the model system as a whole not readily apparent from the nonlinear equations of the model themselves. Methods such as state space reconstruction and sections-of-surface can reveal information implicit in the nonlinear equations. Developing one- and two-dimensional maps from the model equations can also provide this kind of information directly, and are much simpler than the full model equations.
Whereas the first point of contrast is drawn from the practice of physics, the second is logical. After reducing the system to its parts, the next step in the standard approach to understanding, according to Kellert, is to construct a "deductive scheme, which yields a rigorous proof of the necessity (or expectability) of the situation at hand" (1993, p. 91). What Kellert is referring to, here, is the deductive-nomological account of explanation (see Section 2 of the entry on scientific explanation, on the DN model). The approach in chaotic dynamics makes no use of deductive inferences. Specifically, instead of looking at basic principles, propositions, and so on, and making deductive inferences, chaos explanations appeal to computer simulations because of the difficulty or even impossibility of deducing the chaotic behavior of the system from the model equations (e.g., no proof of SD for the Lorenz model based on the governing equations).
The third point of contrast is historical. In contexts where linear superposition holds, a full specification of the instantaneous state plus the equations of motion yield all the information about the system there is to know (e.g., pendulum and projectile motion). Although a full specification of such states is impossible, very small errors in specifying such states lead to very small deviations between model and target system behaviors, at least for short times and good models. By contrast, in nonlinear contexts, where linear superposition fails, a full specification of an instantaneous state of the system plus the equations of motion does not yield all the information there is about the system, for example, if there are memory effects (hysteresis), or the act of measurements introducing disturbances that SDIC can amplify. In the former case, we also need to know the history of the system as well (whether it started out below the critical point or above the critical point, say). So chaos explanations must also take model histories into account.
What kind of understanding is achieved in chaos explanations? Kellert argues we get (1) predictions of qualitative behavior rather than quantitative detail, (2) geometric mechanisms rather than causal processes, and (3) patterns rather than law-like necessity.
Regarding (1), detailed predictions regarding individual trajectories fail rather rapidly for chaotic models when there is any error in specification of the initial state. So, says Kellert, instead we predict global behaviors of models and have an account of limited predictability in chaotic models. But many of these behaviors can be precisely predicted (e.g., control parameter values[9] at which various bifurcations occur, the onset of chaos, the return of n-periodic orbits). (1) amounts to important, but limited insight. On this view we are able to predict when to expect qualitative features of the nonlinear dynamics to undergo a sudden change, but chaos models do not yield precise values of system variables. We get the latter values by running full-blow computer simulations on the full nonlinear model equations, provided the degrees of freedom are reasonable. In this sense, chaos explanations are complimentary to the full model simulation because the former can tell us when/where to expect dynamical changes such as the onset of complicated dynamics in the latter.
Regarding (2), chaos explanation is not a species of causal explanation. That is to say, chaos explanations do not focus on or reveal processes and interactions giving rise to the dynamics; rather, they reveal large-scale geometric features of the dynamics. Kellert argues the kinds of mechanisms on which chaos explanations focus are not causal, but geometric. Part of the reason why he puts things this way is that he views typical causal accounts of explanation as operating in a reductive mode: trace the individual causal processes and their interactions to understand the behavior of the system. But chaos explanations, according to Kellert, eschew this approach, focusing instead on the behavior of systems as wholes. Indeed, chaos explanations tend to group models and systems together as exhibiting similar patterns of behavior without regard for their underlying causal differences. Causal processes are ignored; instead, universal patterns of behavior are the focus. And it is the qualitative information about the geometric features of the model that are key to chaos explanations for Kellert.
Regarding (3), if scientific understanding is only to be achieved via appeal to universal laws expressing nomic necessity—still a strong intuition among many philosophers—then chaos explanations definitely do not measure up. Chaos explanations do not rely on nomic considerations at all; rather, they rely on patterns of behavior and various properties characterizing this behavior. In brief, chaos studies search for patterns rather than laws.
But suppose we change the notion of laws from universal statements of nomic necessity to phenomenological regularities (e.g., Cartwright 1999; Dupré 1993)? Could chaos explanations then be understood as a search for such phenomenological laws at the level of wholes? After all, chaos as a field is not proposing any revisions to physical laws the way relativity and quantum mechanics did. Rather, if it is proposing anything, it is new levels of analysis and techniques for this analysis. Perhaps it is at the level of wholes that interesting phenomenological regularities exist that cannot be probed by microreductionist approaches. But this feature, at least on first blush, may not count against the microreductionist in anything other than an epistemological sense, that is, holistic methodologies are more effective for answering some questions chaos raises.
This dynamical understanding, as Kellert denotes it, achieved by chaos models would suggest that typical causal accounts of explanation are aimed at a different level of understanding. In other words, causal accounts look much more consonant with studying the full nonlinear model. Chaos explanation, by contrast, pursues understanding by using reduced equations derived through various techniques, though still based on the full nonlinear equations. This way of viewing things suggests that there is a kind of unification going on in chaos explanation after all. A set of behavior patterns serves as the explanatory or unificatory features bringing together the appearance of similar features across a very diverse set of phenomena and disciplines (note: Kellert does not discuss unification accounts). This, in turn, suggests a further possibility: A causal account of explanation is more appropriate at the level of the full model, while a unification account perhaps is more appropriate at the level of the chaotic model. The approaches would be complementary rather than competing.
Furthermore, the claim is that study of such chaotic models can give us understanding of the behavior in corresponding actual-world systems. Not because the model trajectories are isomorphic to the system trajectories; rather, because there is a topological or geometric similarity or correspondence between the models and the systems being modeled. This is a different version of the faithful model assumption in that now the topological/geometric features of target systems are taken to be faithfully represented by our chaotic models.
5.2.3 Nothing New under the Sun?
In contrast to Kellert, Peter Smith makes it clear that he thinks there is nothing particularly special about chaos explanations in comparison with explanation in mathematical physics in general (1998, ch. 7). Perhaps it simply is the case that mathematical physics explanations are not well captured by philosophical accounts of explanation and this mismatch—peculiarly highlighted in a catchy field such as chaos—could provide some of the reason for why people have taken chaos explanations to pose radical challenges to traditional philosophical accounts of explanation.
In particular, Smith takes issue with Kellert's view that chaos explanations are, in the main, qualitative rather than quantitative. He points out that we can calculate Lyapunov exponents, bifurcation points as control parameters change, and even use chaos models be predict the values of evolving dynamical variables—"individual trajectory picture"—at least for some short time horizon. So perhaps there is more quantitative information to be gleaned from chaos models than Kellert lets on (this is particularly true if we turn to statistical methods of prediction). Furthermore, Smith argues that standard physics explanations, along with quantitative results, always emphasize the qualitative features of models as well.
We might agree, then, that there is nothing particularly special or challenging about chaos explanations relative to other kinds of explanation in physics regarding qualitative/quantitative understanding. What does seem to be the case is that chaos models—and nonlinear dynamics models generally—make the extraction of usefulness quantitative information more difficult. What is exhibited by methodological approaches in chaos is not that different from what happens in other areas of mathematical physics, where the mathematics is intractable and the physical insight comes with a struggle. Moreover, there is no guarantee that in the future we will not make some kind of breakthrough placing chaos models on a much sounder first principles footing, so there does not seem to be much substance to the claim that chaos explanations are different in kind from other modes of explanation in mathematical physics.
5.3 Taking Stock
Kellert's discussion of "dynamic understanding" and Peter Smith's critical remarks both overlap in their agreement that various robust or universal features of chaos are important for chaos studies The idea of focusing on universal features such as patterns, critical numbers, and so forth suggests that some form of unification account of explanation is what is at work in chaos explanations: group together all examples of chaotic behavior via universal patterns and other features (e.g., period doubling sequences). There is disagreement on the extent to which the methodologies of current chaos research present any radically new challenges to the project of scientific explanation.
Even if there is not something radically new here regarding scientific explanation, the kind of understanding provided by chaos models is challenging to clarify. One problem is that this "dynamic understanding" appears to be descriptive only. That is, Kellert seems to be saying we understand how chaos arises when we can point to a period doubling sequence or to the presence of a strange attractor, for instance. But this appears to be only providing distinguishing marks for chaos rather than yielding genuine insight into what lies behind the behavior, i.e., the cause of the behavior. Kellert eschews causes regarding chaos explanations and there is a fairly straightforward reason for this: The simplified models of chaos appear to be just mathematics (e.g., one dimensional maps) based on the original nonlinear equations. In other words, it looks as if the causes have been squeezed out! So the question of whether causal, unificationist or some other approach to scientific explanation best captures chaos research remains open.
Moreover, since all these simplified models use roughly the same mathematics, why should we think it is surprising that we see the same patterns arise over and over again in disparate models? After all, if all the traces of processes and interactions—the causes—have been removed from chaos models, as Kellert suggests, why should it be surprising that chaos models in physics, biology, economics and social psychology exhibit similar behavior? If it really boils down to the same mathematics in all the models, then what is it we are actually coming to understand by using these models? On the other hand, perhaps chaos studies are uncovering universal patterns that exist in the actual world, not just in mathematics. Identifying these universal patterns is one thing, explaining them is another.
6. Quantum Chaos
Quantum chaos, or quantum chaology as it is better called, is the study of the relationship between chaos in the macroscopic or classical domain and the quantum domain. The implications of chaos in classical physics for quantum systems have received some intensely focused study, with questions raised about the actual existence of chaos in the quantum domain and the viability of the correspondence principle between classical and quantum mechanics to name the most provocative.
Before looking at these questions, there is the thorny problem of defining quantum chaos. The difficulties in establishing an agreed definition of quantum chaos are actually more challenging than for classical chaos (§1). Recall that there were several subtleties involved in attempting to arrive at a consensus definition of classical chaos. One important proposal for a necessary condition is the presence of some form of stretching and folding mechanism associated with a nonlinearity in the system. However, since Schrödinger's equation is linear, quantum mechanics is a linear theory. This means that quantum states starting out initially close remain just as close (in Hilbert space norm) throughout their evolution. So in contrast to chaos in classical physics, there is no separation (exponential or otherwise) between quantum states under Schrödinger evolution. The best candidates for a necessary condition for chaos appear to be missing from the quantum domain.
Instead researchers study the quantization of classical chaotic systems and these studies are known as quantum chaology: "the study of semiclassical, but nonclassical, phenomena characteristic of systems whose classical counterparts exhibit chaos" (Berry 1989, p. 335). It turns out that there are a number of remarkable behaviors exhibited by such quantized systems that are interesting in their own right. It is these behaviors that raise questions about what form chaotic dynamics might take in the quantum domain (if any) and the validity of the correspondence principle. Moreover, these studies reveal further evidence that the relationship between the quantum and classical domains are subtle indeed.
Researchers in quantum chaology have focused on universal statistical properties that are independent of the quantum systems under investigation. Furthermore, studies focus on so-called simple quantum systems (i.e., those that can be described by a finite number of parameters or finite amount of information). The kinds of statistical properties studied in such systems include the statistics of energy levels and semi-classical structures of wave functions. These statistical properties are relevant for quantum state transitions, ionization and other quantum phenomena found in atomic and nuclear physics, solid state physics of mesoscopic systems and even quantum information. Some typical systems studied are quantum billiards (particles restricted to two-dimensional motions), the quantum kicked rotor, a single periodically driven spin and coupled spins. Often, iterated maps are used in investigating quantum chaos just as in classical chaos (§1.2.5 above).
Billiards are a particularly well-studied family of models. Think of a perfectly flat billiard table and assume that the billiard balls bounce off the edges of the table elastically. Such a model table at the macroscopic scale of our experience where the balls and edges are characterized by classical mechanics is called a classical billiard. Lots of analytic results have been worked out for classical billiards so this is makes billiards a very attractive model to study. A chaotic billiard is a classical billiard where the conditions lead to chaotic behavior of the balls. There is a wealth of results for chaotic billiards, too. Such analytical and computational riches have made quantum versions of billiards workhorses for studying quantum chaology as will be seen below. One can produce quantum billiards by using Schrödinger's equation to describe particles reflecting off the boundaries (where one specifies that the wave function for the particles is zero at a boundary), or one can start with the equations describe a classical billiard and quantize the observables (e.g., position and momentum) yielding quantized billiards.
To organize the discussion, isolated systems, where the energy spectra are discrete, will be treated first followed by interacting systems, where energy spectra are continuous. Although whether the energy spectra are discrete or not is not crucial to quantum chaology, whether a quantum system is isolated or not has been argued to be potentially important to whether chaos exists in the quantum realm.
6.1 Does Quantum Chaos Exist? Isolated Systems
One difference between classical chaotic dynamics and quantum dynamics is that the state space of the former supports fractal structure while the state space of the latter does not. A second difference is that classical chaotic dynamics has a continuous energy spectrum associated with its motion. As previously noted, classical chaos is considered to be a property of bounded macroscopic systems. In comparison, the quantum dynamics in bounded, isolated systems has a discrete energy spectrum associated with its motion. Moreover, phenomena such as SDIC could only be possible in quantum systems that appropriately mirror classical system behaviors. From semi-classical considerations, Berry et al. (1979) showed that semi-classical quantum systems (see below for how such systems are constructed) could be expected to mirror the behavior of their corresponding classical systems only up to the Ehrenfest time \(t_{E}\), of the order \(\ln(2\pi/h)\) secs, an estimate also known as the log time reflecting the exponential instability of classical chaotic trajectories. In these semi-classical studies, \(h/2\pi\) often is treated as a parameter that is reduced in magnitude as the classical domain is approached. On this view, the smaller \(h/2\pi\), the more "classical" the system's behavior becomes. For instance, assuming the value of Planck's constant in KMS units, \(t_{E} \sim 80\) secs. As Planck's constant decreases, \(t_{E}\) grows. In nonchaotic classical systems the orbits in state space are well isolated and everything well behaved for very long times. In contrast for bound chaotic systems the orbits start coalescing in increasing numbers on the scale of \(t_{E}\), implying that the semi-classical approximation fails by \(t_{E}\). On the other hand, a Gaussian wave packet centered on a classical trajectory is thought to be able to shadow that trajectory up to \(t_{E}\) before becoming too spread out over the energy surface since \(t_{E}\) is a measure of when quantum wave packets have spread too much to mimic classical trajectories and the Ehrenfest theorem breaks down. So there are two effects at work in semi-classical systems over time: (1) the coalescing of classical chaotic trajectories and (2) the spreading of quantum wave packets. Between the lack of nonlinearity in quantum mechanics and the latter two effects, things look rather bleak for finding close quantum analogs of classical chaos.
While \(t_{E}\) represents an important limit for how long quantum state vectors can be expected to shadow classical trajectories, there are interesting behaviors in the semi-classical quantum models corresponding to classical chaotic systems on longer time scales. By performing some more detailed analysis, Tomsovic and Heller (1993) showed that comparing the full quantum solutions with suitably chosen semi-classical solutions for some billiards problems provided excellent agreement well after \(t_{E}\) including fine details of the energy spectra. For their techniques semi-classical mechanics remains accurate for modeling quantum systems up to a time that scales with \((h/2\pi)^{-1/2}\).
The vast majority of these quantum chaology studies focus on three questions:
- Can classically chaotic systems be quantized?
- Are there any quantum mechanical manifestations, "precursors," of classical chaos?
- Is there a rigorous distinction between chaotic and non-chaotic quantum systems?[10]
The first two questions focus on different directions of research, both related to what is known as semi-classical mechanics. In the first, investigation starts with a classical chaotic system and seeks to quantize it to study its quantum behavior. To quantize a classical model, one replaces functions in the equations of motion with their corresponding quantum operators. Here, there are various results demonstrating that strongly ergodic classical billiards, when quantized, exhibit quantum ergodicity. But this is not the same as showing that a classical chaotic system, when quantized, exhibits chaotic behavior. There are no examples of the latter due to the reasons listed at the beginning of this subsection.
Furthermore, there are interesting numerical results on quantum interference in quantized classical billiards (Casati 2005). Consider a double slit with the source enclosed in a two-dimensional wave resonator with the shape of a classical billiard. Adjust the Gaussian wave packet's initial average energy to be one 1600th of an excited state of the quantized billiard and send it toward the double slit opening of the resonator. Let the slit width be three De Broglie wavelengths, and suppose that the wave packet is sharply peaked in momentum so that its spatial spread, by the Heisenberg relations, is the width of the resonator. If the shape of the resonator corresponds to a classical chaotic billiard, then there is almost no quantum interference. In the classical case, the multiply reflected waves would become randomized in phase. On the other hand, if the shape of the resonator corresponds to a classical regular billiard, then the well-known interference patterns emerge. So depending on whether the classical billiard is chaotic or not determines whether the quantized quantum analogue exhibits interference.
The second question starts with a quantum system that has some relationship with a classical chaotic system via an appropriate semi-classical limit. The classical-to-quantum direction often follows the pioneering work of Martin Gutzweiller (1971) in quantizing the classical chaotic system. The quantum-to-classical direction is much more difficult and fraught with conceptual problems. Standard approaches, here, are to start with a quantum analogue to a classical chaotic system and then derive a semi-classical system that represents the quantum system in some kind of classical limit (Berry 1987 and 2001; Bokulich 2008). This work results in statistics of suitably normalized energy levels for the semi-classical systems with universal features. For classical systems that behave non-chaotically, the energy levels of the semi-classical system approximate a Poisson distribution, where small spacings dominate. In contrast when the classical system behaves chaotically, the energy levels of the semi-classical system take on a distribution originally derived by Eugene Wigner (1951) to describe nuclear energy spectra (for discussion see Guhr et al. 1998). These latter distributions depend only on some symmetry properties (e.g., the presence or absence of time-reversal symmetry in the system).[11] Moreover, the presence of periodic orbits in the analog classical systems largely determine the properties of semi-classical systems (Berry 1977).
Interestingly, many classically chaotic models systems also display universal energy level fluctuations that are well described by Wigner's methods (Casati, Guarneri and Valz-Gris 1980; Bohigas, Giannoni and Schmit 1984). This has led to the quantum chaos conjecture:
(Quantum Chaos Conjecture)
The short-range correlations in the energy spectra of semi-classical quantum systems which are strongly chaotic in the classical limit obey universal fluctuation laws based on ensembles of random matrices without free parameters.
This conjecture is motivated by the accumulated evidence over the decades that the energy spectra of very simple non-integrable classically chaotic systems contain universal level fluctuations described by random matrix theory. Given random matrix theory's successful application to nuclear spectra and these classical results, the question of whether there were analog results for quantum systems with chaotic systems as an appropriate limit seems reasonable. The conjecture basically means that the energy spectra for the semi-classical analogues of classical chaotic systems are structurally the same as those classical systems. This conjecture remains unproven, though it appears to hold for the case of classical chaotic billiards and their semi-classical counterparts. Since this is a conjecture about semi-classical systems, this means that the structure of the energy spectra of semi-classical systems is strictly dependent on chaos in the corresponding classical systems not on any chaotic behavior in quantum or semi-classical systems.
One can raise serious questions about these quantum-to-classical studies, however. The semi-classical systems are derived using various asymptotic procedures (Berry 1987 and 2001), but these procedures do not yield the actual classical systems that are supposed to be the limiting cases of the quantum systems. More importantly, the actual kinds of limiting relations between the quantum and classical domains are different than are typically considered in semi-classical approaches (§6.3 below). The actual relationship between the mathematical results and actual quantum and classical physical systems is tenuous at best leaving us, again, with the worry that chaos is an artifact of the mathematics (§5). One of the reasons the quantum chaos conjecture remains unproven likely is that inappropriate notions of "the classical limit" are being used. Even though the energy level statistics for quantum billiards in the semi-classical counterparts to classical billiard systems share universal properties, the actual behavior of the trajectories in the two systems is substantially different (under Schrödinger evolution Hilbert space vectors never diverge from one another).
Another fundamental problem is that classical chaos is a function of nonlinearities whereas Schrödinger's equation describing quantum systems is linear. Empirical investigation of quantum chaology, hence, usually focuses on externally driven quantum systems (see next section) and scattering processes (e.g., quantum billiards). The focus in these studies is on the unpredictability of the time evolution of such systems and processes. Although unpredictability is a feature of classical chaotic systems, there are many reasons why the time evolution of quantum systems may be as unpredictable (e.g., if commuting observables undergo complicated dynamics). It is not clear that unpredictability in externally driven quantum systems and scattering processes is due to any form of chaos.
Quantum systems do sometimes exhibit bifurcations. For instance, rotating molecules under some circumstances will undergo several consecutive qualitative changes that are interpreted as bifurcations (Zhilinskií 2001). Whether there is a series of bifurcations in such systems that could eventually lead to a transition to some form of quantum chaotic behavior is currently unknown.
At best, quantum chaology in isolated systems has produced results that have interesting relationships with integrable and non-integrable classical systems and some important experimental results (e.g., Bayfield and Koch 1974; Casati, Chirikov, Izrailev and Ford 1979; Fishman, Grempel and Prange 1982; Casati, Chirikov and Shepelyanski 1984; Berry 2001). These relationships are all statistical as indicated. One issue with studying isolated, closed quantum systems is that the state spaces of these systems do not allow the formation of the state-space structures typically associated with classical chaotic systems. There are some exceptions discussed in the literature, but it is actually ambiguous if these are genuine cases of chaos. One example discussed in the literature is a quantum Hamiltonian operator for an \(N\)-dimensional torus: \(\bfrac{1}{2}(g_{k} n_{k} + n_{k} g_{k})\), where \(n_{k} = -i\partial / \partial \theta_{k}, \theta_{k}\) is an angle variable, and \(d\theta_{i} /dt = g_{i}(\theta_{k})\) for \(i, k = 1, 2,3,..., N\) (Chirikov, Izrailev and Shepelyanski 1988, p. 79). The probability density for momentum grows exponentially fast, which seems to parallel SDIC for trajectories in the classical case. Again, it is far from clear that this is chaos; there is no principled reason for considering the exponential growth in some quantity as a mark of chaos (recall the example in the first paragraph of §1.2.6 above).
Building on the numerical results of the double-slit/billiard wave resonator described above, it may be possible to apply quantum chaology to the quantum measurement problem. Typically, models for quantum measurement describe the destruction of coherent quantum states as an effect of external noise or the environment. These quantum chaology results could allow the development of a dynamical theory of quantum decoherence due to the interaction between a classical chaotic (or at least non-integrable) system and coherent quantum states producing the incoherent mixtures observed in measurement devices. These considerations lead us to interacting systems.
6.2 Does Quantum Chaos Exist? Interacting Systems
The failure to find the features of classical chaos in quantum systems is usually diagnosed as being due to the linear nature of Schrödinger's equation (classical chaos appears to require nonlinearity as a necessary condition). And the evidence from isolated quantum systems substantiates this diagnosis as just discussed. What about interacting quantum systems (which sometimes get called open quantum systems)? At first glance, one can argue that the linearity of Schrödinger's equation implies that nearby quantum states will always remain nearby as they evolve in time. However, some alternative possibilities for possible chaotic behavior have been proposed for interacting quantum systems.
Fred Kronz (1998, 2000) has argued that focusing on the separable/nonseparable Hamiltonian distinction is more appropriate than nonlinearity for the question of quantum chaos (1.2.7 Taking Stock above). Although Schrödinger's equation is linear, there are many examples of nonseparable Hamiltonians in quantum mechanics. A prime example would be the Hamiltonian describing an interaction between a measurement device and a quantum system. In such situations, the quantum system-measurement apparatus compound system can evolve from a tensor product state to a nonseparable entangled state represented by an irreducible superposition of tensor product states. A second ubiquitous example would be the famous Einstein-Podolsky-Rosen correlations. Although many, such as Robert Hilborn (1994, 549–569), have argued that the unitary evolution of quantum systems makes SDIC impossible for quantum mechanics, these arguments do not take into account that interacting quantum systems typically have nonseparable Hamiltonians.
For interacting quantum systems, Schrödinger's equation is no longer valid and one typically turns to so-called master equations to describe evolution (Davies 1976). Such equations typically have nonseparable Hamiltonians. In general, the time evolution of the components of such interacting systems is not unitary meaning that there is no formal prohibition against SDIC. Moreover, an important contrast between isolated and interacting quantum systems is that while the former have discrete energy spectra, the latter have continuous spectra. A continuous energy spectrum is characteristic of classical systems. Nevertheless, work in interacting quantum systems largely has only uncovered the same kinds of universal statistical characteristics of energy spectra and fluctuations as found in isolated systems (e.g., Guhr, Müller-Groeling and Weidenmüller 1998; Ponomarenko, et al. 2008; Filikhin, Matinyan and Vlahovic 2011).
It is often the case that the quantum chaology literature uses a broader notion of chaos as behavior that "cannot be described as a superposition of independent one-dimensional motions" (Ponomarenko, et al. 2008, p. 357); in other words, a form of inseparability. Still, the chaology in interacting quantum systems looks to be the same as in isolated systems: "Quantum mechanically, chaotic systems are characterized by distinctive statistics of their energy levels, which must comply with one of the Gaussian random ensembles, in contrast to the level statistics for the nonchaotic systems described by the Poisson distribution" (Ponomarenko, et al. 2008, p. 357). This is largely due to the fact that quantum chaology is closely tied to universal statistical patterns in quantum systems that share some relationship with classical chaotic counterpart systems.
One of the measures used to detect chaotic behavior in classical systems is a positive Kolmogorov entropy, which can be related to Lyapunov exponents (e.g., Atmanspacher and Scheingraber 1987). Unfortunately, there are no appropriate analogous for Lyapunov exponents in quantum systems. There are alternative entropy measures that could be used, for instance, the von Neumann or Connes-Narnhofer-Thirring entropies. However, there are currently many open questions about which, if any, of these entropy measures is the appropriate quantum analog (likely they are each appropriate for particular research purposes). Moreover, while these measures have a relationship to the statistics of energy levels and states characteristic of quantum chaology, there currently are no other known features of quantum systems that these measures could relate to chaotic behavior observed in classical trajectories.
There is an interesting physical model of a charged particle in a unit square with periodic boundary conditions with an external electromagnetic field that occasionally gives it a kick (turns on and off). Mathematically this model is a generalization of the quantized Arnold cat map (Arnold and Avez 1968; Weigert 1990; Weigert 1993). Physically it represents a charged particle confined to an energy surface shaped like a torus that receives kicks from an external field. The classical model has trajectories that exhibit the stretching and folding process that seems to be a necessary condition for chaos, has positive Lyapunov exponents, and is algorithmically complex[12], one of the measures used to detect classical chaos. Its trajectories have many of the marks of chaos. For the quantum model, the kick of the electromagnetic field has the effect of mapping the quantum labels of state vectors that are initially close together to labels which do not necessarily ever come close again. This is somewhat reminiscent of the divergence of classical chaotic trajectories except that it is the change in the state labels that plays the role of the classical trajectories. This leads to an absolutely continuous quasi-energy spectrum (the quasi-energy is defined as the set of numbers representing the "energy" in the evolution operator acting on state vector labels). The expectation value of the particle position becomes unpredictable with respect to the initial state label after long times and one can show that the sequence of shifts of the quantum state labels is algorithmically complex. Moreover, a "distance" between the labels can be defined that increases exponentially with time.
This is the most convincing example in quantum chaology of behavior analogous to classical chaos. However, there are issues that raise questions about whether the behavior of the sequences of quantum state labels is enough to qualify the system as chaotic. For one thing, the quantum chaos conjecture is inapplicable to this system due to the continuous spectrum of the quasi-energy. More importantly, as pointed about above, exponential divergence is neither necessary nor sufficient to characterize a system as chaotic, and neither is algorithmic complexity. There are many examples of systems that are algorithmically complex but are not chaotic. Long randomly generated bit strings, no matter how they were obtained, are algorithmically complex but need not have any relationship to chaos. The behavior of the quantum labels for the kicked particle is irregular to be sure, but the actual temporal evolution of the state vectors is algorithmically compressible, so not irregular in any way.
6.3 The Validity of the Correspondence Principle
The kind of behavior observed in quantum chaology involves the statistics of energy states in quantum systems that have some kind of relationship to classical chaotic systems (e.g., by quantizing the latter systems). Important features of classical chaos, such as SDIC and the period doubling route to chaos, appear to be absent from quantum systems. This situation has led to arguments that the correspondence principle between quantum and classical mechanics fails and that the former may be incomplete (Ford 1992).
The correspondence principle can be understood broadly to mean that as a quantum system system is scaled up to macroscopic size, its behavior should become more like a classical system. Alternatively, the behavior of a quantum model should reproduce the behavior of macroscopic classical models in the limit of large quantum numbers. The correspondence principle is sometimes conceived as letting Planck's constant go to zero. Nevertheless, all these conceptions are terribly inadequate. Since \(h\) is a constant of nature, it can never change value, much less go to zero. One always has to speak of relevant limits of ratios of the classical to quantum actions, for example, which always involve Planck's constant. Moreover, these limits are singular, meaning that the smooth behavior of a quantity or pattern is disrupted, often by becoming infinite (Friedrichs 1955; Dingle 1973; Primas 1998). So there is no straightforward sense in which quantum models become increasingly similar to macroscopic systems as quantum numbers get large.
Joseph Ford offers a different construal of the correspondence principle: "any two valid physical theories which have an overlap in their domains of validity must, to relevant accuracy, yield the same predictions for physical observations." In the case of quantum and Newtonian mechanics, this means that "quantum mechanics must, in general agree with the predictions of Newtonian mechanics when the systems under study are macroscopic" (1992, p. 1087). Unfortunately, he gives no discussion of what "domains of validity" mean or in what sense quantum and Newtonian mechanics have some overlap in their domains of validity. What he claims in his American Journal of Physics article is that "The very essence of correspondence lies in the notion that quantum mechanics can describe events in the macroscopic world without any limit taking. Were this not the case, then there would be no overlap in the quantal and classical regions of validity" (1992, p. 1088). Sir Michael Berry is even more direct: "all systems," even our orbiting moon, "obey the laws of quantum mechanics" (Berry 2001, p. 42). The upshot for chaos is that "if there is chaos (however defined) in the macroscopic world, quantum mechanics must also exhibit precisely the same chaos, else quantum mechanics is not as general a theory as popularly supposed" (Ford 1992, p. 1088).
As seen above, classical chaotic behavior is not recovered in quantum chaology, and this leads to a dilemma: Either the correspondence principle is false or quantum mechanics is incomplete. Ford, as would most physicists, rejects the first horn of the dilemma. Therefore, the problem must lie with quantum mechanics: Its lack of chaos reveals some incompleteness in the theory. Something is missing.
This dilemma is false, however. The way Ford (and to some degree Berry among others) describes things bespeaks a common misconception of the relationship between the quantum and classical domains. Much as he makes of the subtlety of limiting relations—and they are much more subtle than he realizes—his discussion of the correspondence principle actually turns on an overly simple relationship between the quantum and classical domains. That overly simple relationship presupposes that quantum mechanics fully explains classical phenomena, or, alternatively, that quantum mechanics reduces the classical domain in an appropriate limit. Under such a presupposition, if classical chaos either does not exist in quantum mechanics or if the latter cannot explain or reproduce classical chaos, then it appears that there is some inadequacy with quantum mechanics.
The relationship between the quantum and classical domains is nontrivial. First, it does not involve a "classical limit," but a series of limits of the ratio of quantum observables involving Planck's constant and other physical observables going to zero (e.g., relevant classical and quantum actions), or limits involving the separation of nuclear and electronic frames of motion (in the case of chemistry) among others. All of these limits involve singular asymptotic series; hence, the relationship between quantum phenomena and classical phenomena is not one involving anything like bridge laws relating the two domains as Nagelian and other forms of reduction would require. There is a change in the character of the states and observables going from the quantum to the classical domains (Bishop, 2010b). The classical states and observables are neither a function of nor straightforwardly related to intrinsic states and observables in quantum mechanics.
Second, even starting with the quantum domain, there are different classical worlds that result from taking these various limits in different orders. Since these limits correspond to different physical transitions, changing the order of the limits changes the order of physical transitions yielding physically inequivalent macroscopic domains. Given the physical incompatibility among these different macroscopic worlds, the actual physical transitions between the quantum and classical must occur in a particular order to recover the classical domain of our experience.
Of course, there is much discussion of the "approximately classical" or "quasi-classical" trajectories for quantum systems that can be derived from semi-classical considerations (Berry 1987 and 2001). But such quasi-classical behavior is exhibited only for limited times (except for overly idealized models) and under very special initial conditions (Pauli 1933, p. 166) for ground states only (excited energy eigenstates never show classical behavior). Appeal to Ehrenfest's theorem is of no help, here, because all this theorem guarantees for such very special, short-lived dynamics is that the usual physics practice of averaging the values of the quantum-mechanical observables tends to wash out the errors or differences between the classical and quantum calculations for contextually relevant situations and times. Moreover, the theorem is neither necessary nor sufficient for classical behavior. For instance, applying Ehrenfest's theorem to a quantum harmonic oscillator yields average quantities for the position and momentum that track with the classical quantities for some brief time. Yet, the quantum oscillator's discrete states yield thermodynamic properties very different from a classical oscillator. So satisfying the theorem is insufficient to guarantee classical behavior.
Third, the emergence of our classical world is not merely a matter of environmental decoherence (e.g., Omnés 1994; Berry 2001; Wallace 2012). For one thing, there is no context-free limit of infinitely many degrees of freedom because this limit always has uncountably infinitely many physically inequivalent representations. Moreover, it is simply false that an improper mixture of quantum states "allows one to interpret the state of the [quantum] system in terms of a classical probability distribution," such that "it is useful to regard 'mixed states' as effectively classical," so that "one can interpret the system described by [a nonpure density operator] in terms of a classical 'mixture' with the exact state of the system unknown to the observer" (Zurek 1991, 46–47). Impure quantum states can be interpreted as classical mixtures if and only if their components are described by disjoint states. For a classical mixture of two pure states (e.g., water and oil), the pure states are disjoint if and only if there exists a classical observable such that the expectation values with respect to these states are different. It is this disjointness that makes it possible to distinguish states in a classical manner.
In summary, there is nothing in the quantum domain by itself that determines the character of the classical domain (though the former provides some necessary conditions for the latter). Hence, classical chaos, along with many other classical features, is emergent in a more complex, subtle sense than Ford and others allow. The correspondence principle must reflect emergent classicality if it is to be a viable principle, which means that the implicit assumption of reductionism in Ford's discussions of quantum chaology should be abandoned. Once the reductionist assumption is removed, the disparity between quantum chaology and classical chaos no longer calls an appropriately formulated correspondence principle into question. This resolves the first horn of the dilemma.
The second horn of the dilemma likewise is resolved. There is no reason to suspect that there is some kind of inadequacy in quantum mechanics if features such as chaos are emergent in the classical domain. Neither the generality nor the validity of quantum mechanics is in question. Nor does the complex, subtle emergent relationship between the quantum and classical domains imply that the two domains are nonoverlapping or disjoint. Rather, the overlap between the quantum and classical is partial and nontrivial. Quantum mechanics is universally applicable, but this in no way implies that it alone universally governs classical behavior. It contributes some of the necessary conditions for classical properties and behaviors, but no sufficient conditions. One indicator of this is that classical mechanics is formulated in terms of continuous trajectories of individual particles through spacetime, while quantum mechanics is formulated in terms of probabilities and wave functions. There are deep conceptual differences between the classical and the quantum.[13] This suggests that we should not expect individual continuous trajectories to result from quantum mechanics in contextually inappropriate limits nor that quantum mechanics should exhibit the full range of classical behaviors, contrary to Ford and others. Instead, we should expect that quantum probabilities recover the classical probabilities in the contextually appropriate situations and that there should be some interesting relationships between quantum and classical properties and behaviors. The interesting statistical regularities discovered in quantum chaology fit with this emergent, nontrival overlapping relationship nicely.
7. Some Broader Implications of Chaos
There have been some discussions regarding the wider implications of chaos for other domains of philosophical inquiry. Three of the more thought-provoking ones will be surveyed here.
7.1 Chaos and Determinism
Recall that mathematically, chaos is a property of dynamical systems which are deterministic (§1.2.1). Since the 18th century, the best models of and support for metaphysical determinism were thought to be the determinism of theories and models in physics. But this strategy is more problematic and subtle than has been typically realized (e.g., due to the difficulties with faithful models, §3.). So perhaps it is not so surprising that some have argued that chaos reflects some form of indeterminism; hence, the world is not metaphysically deterministic. Of course, chaotic systems are notorious for their unpredictability, and some such as Karl Popper (1950) have argued that unpredictability implies indeterminism. Yet this is to identify determinism (an ontological property) with predictability (an epistemic property).
An example of someone who has pushed the claim that chaotic behavior implies that determinism fails for our word is physicist turned Anglican priest, John Polkinghorne: "The apparently deterministic proves to be intrinsically unpredictable. It is suggested that the natural interpretation of this exquisite sensitivity is to treat it, not merely as an epistemological barrier, but as an indication of the ontological openness of the world of complex dynamical systems" (1989, p. 43). Giving a critical realist reading of epistemology and ontology, Polkinghorne seeks to link the epistemological barrier with an ontological failure of determinism because of ontological openness to influences not fully accounted for in our physics descriptions. Nevertheless, the mathematical properties of dynamical systems (e.g., their deterministic character) present a serious problem with this line of reasoning. Determinism as unique evolution appears to be preserved in our mathematical models of chaos, which serve as our ontic descriptions of chaotic systems.[14]
What would it take to raise questions about the determinism of actual-world systems? For nonlinear dynamical systems, their presumed connection with target systems is one place to start. Mathematical modeling of actual-world systems requires distinctions between variables and parameters as well as between systems and their boundaries. However, where linear superposition is lost such distinctions become problematic (Bishop 2010a). This situation raises questions about our epistemic access to systems and models in the investigation of complex systems, but also raises questions about inferring the supposed determinism of target systems based on these models. Moreover, if the system in question is nonlinear, then the faithful model assumption (§1.2.3) raises difficulties for inferring the determinism of the target system from the deterministic character of the model.
Consider the problem of the mapping between the model and the target system. There is no guarantee that this mapping is one-to-one even for the most faithful model. The mapping may actually be a many-to-one relation or a many-to-many relationship. A one-to-one relationship between a deterministic model and target system would make the inference from the deterministic character of our mathematical model to the deterministic character of the target system more secure. However, a many-to-one mapping raises problems. One might think this can be resolved by requiring the entire model class in a many-to-one relation be deterministic. Such a requirement is nontrivial, though. For instance, it's not uncommon for different modeling groups to submit proposals for the same project, where some propose deterministic models and others propose nondeterministic models. Nonlinear models render any inferences from physics to metaphysical determinism shaky at best.
7.2 Free Will and Consciousness
A number of authors have looked to quantum mechanics to help explain consciousness and free will (e.g., Compton 1935; Eccles 1970; Penrose 1991, 1994 and 1997; Beck and Eccles 1992; Stapp 1993; Kane 1996; quantum consciousness). Still it has been less clear to many that quantum mechanics is relevant to consciousness and free will. For example, an early objection to quantum effects influencing human volitions was offered by philosopher J. J. C. Smart (1963, pp. 123–4).[15] Even if indeterminism was true at the quantum level, Smart argued that the brain remains deterministic in its operations because quantum events are insignificant by comparison. After all a single neuron is known to be excited by on the order of a thousand molecules, each molecule consisting of ten to twenty atoms. Quantum effects though substantial when focusing on single atoms are presumed negligible when focusing on systems involving large numbers of molecules. So it looks like quantum effects would be too insignificant in comparison to the effects of thousands of molecules to play any possible role in consciousness or deliberation.
Arguments such as Smart's do not take into consideration the possibility for amplifying quantum effects through the interplay between SDIC at the level of the macroscopic world on the one hand and quantum effects on the other (see §4). SD arguments purport to demonstrate that chaos in classical systems can amplify quantum fluctuations due to sensitivity to the smallest changes in initial conditions. Along these lines suppose (somewhat simplistically) the patterns of neural firings in the brain correspond to decision states. The idea is that chaos could amplify quantum events causing a single neuron to fire that would not have fired otherwise. If the brain (a macroscopic object) is also in a chaotic dynamical state, making it sensitive to small disturbances, this additional neural firing, small as it is, would then be further amplified to the point where the brain states would evolve differently than if the neuron had not fired. In turn these altered neural firings and brain states would carry forward such quantum effects affecting the outcomes of human choices.
There are several objections to this line of argument. First, the presence of chaos in the brain and its operations is an empirical matter that is hotly debated (Freeman and Skarda 1987; Freeman 1991, 2000; Kaneko, Tsuda and Ikegami 1994 pp. 103–189; Vandervert 1997; Diesmann, Gewaltig and Aertsen 1999; Lehnertz 2000; Van Orden, Holden and Turvey 2003 and 2005; Aihara 2008; Rajan, Abbott and Sompolinsky 2010). It should be pointed out, however, that these discussions typically assume SD or Chaos\(_{\lambda}\) as the definition of chaos. All that is really needed for sensitivity to and amplification of quantum effects in the brain is the loss of principle of superposition found in nonlinear systems. Second, these kinds of sensitivity arguments depend crucially on how quantum mechanics itself and measurements are interpreted as well as the status of indeterminism (§4). Third, although in the abstract sensitivity arguments seem to lead to the conclusion that the smallest of effects can be amplified, applying such arguments to concrete physical systems shows that the amplification process may be severely constrained. In the case of the brain, we currently do no know what constraints on amplification exist.
An alternative possibility avoiding many of the difficulties exhibited in the chaos+quantum mechanics approach is suggested by the research on far-from-equilibrium systems by Ilya Prigogine and his Brussels-Austin Group (Bishop 2004). Their work purports to offer reasons to search for a different type of indeterminism in both micro and macrophysical domains.
Consider a system of particles. If the particles are distributed uniformly in position in a region of space, the system is said to be in thermodynamic equilibrium (e.g., cream uniformly distributed throughout a cup of coffee). In contrast, if the system is far-from-equilibrium (nonequilibrium) the particles are arranged so that highly ordered structures might appear (e.g., a cube of ice floating in tea). The following properties characterize nonequilibrium statistical systems: large number of particles, high degree of structure and order, collective behavior, irreversibility, and emergent properties. The brain possesses all these properties, so that the brain can be considered a nonequilibrium system (an equilibrium brain is a dead brain!).
Let me quickly sketch a simplified version of the approach to point out why the developments of the Brussels-Austin Group offer an alternative for investigating the connections between physics, consciousness and free will. Conventional approaches in physics describe systems using particle trajectories as a fundamental explanatory element of their models, meaning that the behavior of a model is derivable from the trajectories of the particles composing the model. The equations governing the motion of these particles are reversible with respect to time (they can be run backwards and forwards like a film). When there are too many particles involved to make these types of calculations feasible (as in gases or liquids), coarse-grained averaging procedures are used to develop a statistical picture of how the system behaves rather than focusing on the behavior of individual particles.
In contrast the Brussels-Austin approach views nonequilibrium systems in terms of nonlinear models whose fundamental explanatory elements are distributions; that is to say, the arrangements of the particles are the fundamental explanatory elements and not the individual particles and trajectories.[16] The equations governing the behavior of these distributions are generally irreversible with respect to time. In addition focusing exclusively on distribution functions opens the possibility that macroscopic nonequilibrium models are irreducibly indeterministic, an indeterminism that has nothing to do with ignorance about the system. If so, this would mean probabilities are as much an ontologically fundamental element of the macroscopic world as they are of the microscopic and are free of the interpretive difficulties found in conventional quantum mechanics.
One important insight of the Brussels-Austin Group's shift away from trajectories to distributions as fundamental elements is that explanation also shifts from a local context (set of particle trajectories) to a global context (distribution of the entire set of particles). Systems acting as a whole may produce collective effects that are not reducible to a summation of the trajectories and subelements composing the system (Bishop 2004 and 2012). The brain exhibits this type of collective behavior in many circumstances (Engel, et al. 1997) and the work of Prigogine and his colleagues gives us another tool for trying to understand that behavior. Moreover, nonlinear nonequilibrium models also exhibit SDIC, so there are a number of possibilities in such approaches for very rich dynamical description of brain operations and cognitive phenomena (e.g., Juarrero 1999; Chemero and Silberstein 2008). Though the Brussels-Austin approach to nonequilibrium statistical mechanics is still speculative and contains some open technical questions, it offers an alternative for exploring the relationship between physics, consciousness and free will as well as pointing to a new possible source for indeterminism to be explored in free will theories.
Whether approaches applying chaotic dynamics to understanding the nature of consciousness and free will represent genuine advances remains an open question. For example, if the world is deterministic, then the invocation of SDIC in cognitive dynamics (e.g., Kane 1996) may provide a sophisticated framework for exploring deliberative processes, but would not be sufficient for incompatibilist notions of freedom. On the other hand, if indeterminism (quantum mechanical or otherwise) is operative in the brain, the challenge still remains for indeterminists such Robert Kane (1996) to demonstrate that agents can effectively harness such indeterminism by utilizing the exquisite sensitivity provided by nonlinear dynamics to ground and explain free will. Questions about realism and explanation in chaotic dynamics (§5) are relevant here as well as the faithful model assumption.
7.3 Human and Divine Action in a Nonlinear World
There has also been much recent work applying the perspective of dynamical systems to cognition and action, drawing explicitly on such properties as attractors, bifurcations, SDIC and other denizens of the nonlinear zoo (e.g., van Gelder 1995; Kelso 1995; Port and van Gelder 1995; Juarrero 1999; Tsuda 2001). The basic idea is to deploy the framework of nonlinear dynamics for interpreting neural and cognitive activity as well as complex behavior. It is then hoped that patterns of neural, cognitive and human activity can be explained as the results of nonlinear dynamical processes involving causal interactions and constraints at multiple levels (e.g., neurons, brains, bodies, physical environments). Such approaches are highly suggestive, but also face challenges. For instance, as mentioned in the previous section, the nature of neural and cognitive dynamics is still much disputed. Ultimately, it is an empirical matter whether these dynamics are largely nonlinear or not. Moreover, the explanatory power of dynamical systems approaches relative to rival computational approaches has been challenged (e.g., Clark 1998). Again, questions about realism and explanation in chaotic dynamics (§5) are relevant here as well as the faithful model assumption.
Furthermore, Polkinghorne (among others), as previously noted, has proposed interpreting the randomness in macroscopic chaotic models and systems as representing a genuine indeterminism rather than merely a measure of our ignorance (1991, pp. 34–48). The idea is that such openness or indeterminism is not only important to the free will and action that we experience (pp. 40–1), but also for divine action in the world (e.g., Polkinghorne 1989; §7.1). In essence the sensitivity to small changes exhibited by the systems and models studied in chaotic dynamics, complexity theory and nonequilibrium statistical mechanics is taken to represent an ontological opening in the physical order for divine activity. However the sensitivity upon which Polkinghorne relies would also be open to quantum influences whether deterministic or indeterministic. Furthermore, as mentioned previously in connection with the Brussels-Austin program, much rides on whether a source for indeterminism in chaotic behavior can be found. If Polkinghorne's suggestion amounts to simply viewing the world as if chaos harbors indeterminism, then it seems that this suggestion doesn't yield the kind of divine action he seeks.
7. Conclusion
Chaos and nonlinear dynamics are not only rich areas for scientific investigation, but also raise a number of interesting philosophical questions. The majority of these questions, however, remain thoroughly under studied by philosophers.
Appendix: Global Lyapunov Exponents
Thinking With Mathematical Models Problem 2.4 Answers
Source: https://plato.stanford.edu/entries/chaos/
Posted by: gilliamwough1983.blogspot.com

0 Response to "Thinking With Mathematical Models Problem 2.4 Answers"
Post a Comment